4

Use rook polynomials to count the number of permutations of $(1,2,3,4)$ in which $1$ is not in the second position, $2$ is not in the fourth position, and $3$ is not in the first or fourth position. How do we solve this one? Do we first calculate the rook polynomials of forbidden positions and then subtract?

Batominovski
  • 49,629
user180588
  • 61
  • What is the board you're working with? Where are these "first, second, third, fourth" positions? Providing a diagram would get you more responses from here. – Train Heartnet Oct 03 '14 at 06:00
  • The question doesn't mention any other thing but I think it's supposed to be 4 by 4 board and #1 cannot be in the second position of 1st row, 2 cannot be in the 4th position of 2nd row and 3 cannot be in the 1st or 4th position in 3rd row. I don't know if that helps. – user180588 Oct 03 '14 at 06:26
  • Do you know the formula that gives the number of restricted permutations of $[n]$ as $\Sigma_{k=0}^n(-1)^k r_k(B)(n-k)!$ where $r_k(B)$ is the coefficient of $x^k$ in the rook polynomial for the forbidden board? I hesitate to present this is an answer since it strictly uses only the coefficients of the rook polynomial. – Leen Droogendijk Oct 03 '14 at 10:52

1 Answers1

9

The easiest thing to do would be to draw out your diagram first. Given the information in the problem as stated, a reasonable chess board would be given as

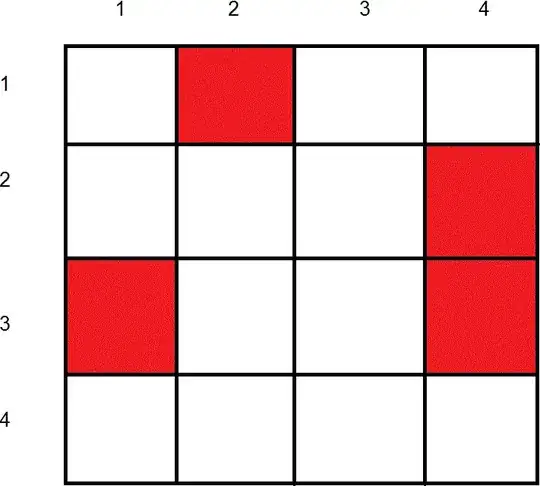
Image of Chess board without re-ordering

For this chess board, the numbers on the left column represent the numbers to be permuted, the numbers along the top row represent the positions that a number can go to. A square that is shaded red is a forbidden region (for example, the square at row 1, column 2 is forbidden since you state in the problem description that the number 1 can not go to position #2).

We can reorganize the columns to make a chess board that is easier to work with like the one below.

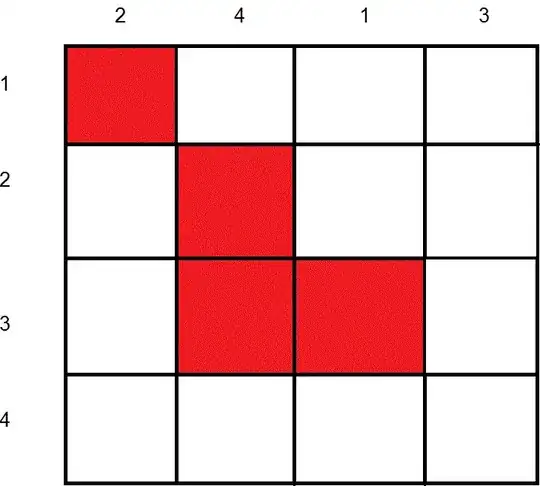
Image of chess board with reordered columns.

Seeing as there are far fewer forbidden positions than allowed positions, your guess that counting the number of ways to place a number into a forbidden position, and then subtracting from the total number of ways to permute the numbers is actually a good idea.

Because of the way I reordered the chess board, determining the rook polynomials for the forbidden regions is relatively easy.

The rook polynomial for the red square at row 1, column 2 is (1 + x). The rook polynomial for the other forbidden region is (1 + 3x + x2). Seeing as both of these regions are disjoint (meaning that neither region shares a row or a column), we simply multiply both polynomials together, yielding

1 + 4x + 4x2 + x3

We now use the Principle of Inclusion and Exclusion to count the number of possible arrangements where no number gets sent to a forbidden position.

Let rk be the coefficient of xk in the rook polynomial (1 + 4x + 4x2 + x3).

Without regard to forbidden positions, there are r0(4!) = 1 * 4! ways to permute the numbers.

We now subtract off the number of permutations where at least one number is in a forbidden position, given by r1(3!) = 4*3!.

But we subtracted off twice as many permutations with at least 2 numbers in forbidden positions, so we must add on one of each, given by r2(2!) = 4*2!.

In adding on the previous term, we have twice counted the number of permutations with 3 of the numbers in forbidden positions, so we must subtract off those permutations one more time, given by r3(1!) = 1*1!.

The final answer is given by (1 * 4!) - (4 * 3!) + (4 * 2!) - (1 * 1!).

We could simplify: (1 * 4!) - (4 * 3!) + (4 * 2!) - (1 * 1!) = 24 - 24 + 8 - 1 = 7.

There are a total of 7 ways to permute the numbers 1,2,3,4 such that 1 does not go to position #2, 2 does not go to position #4, and 3 does not go to position #1 or position #4.

Jacob Hiance
  • 91
  • 1