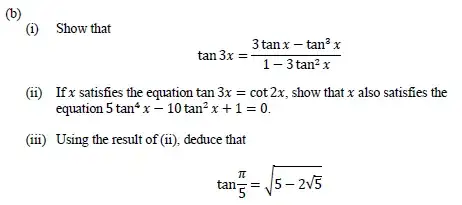Consider an isosceles triangle $ABC$, having its vertex angle $\hat{C}$ equal to $\pi/5$, so the base angles $\hat{A}$ and $\hat{B}$ are $2\pi/5$. Draw the bisector of angle $\hat{B}$ meeting $AC$ in $D$.
Then the triangle $ADB$ is similar to $ABC$. Call $l$ the length of $AC$ and $x$ the length of $AB$. Then $BD$ and $DC$ also have length $x$ and $l\cos2\pi/5=x/2$.
By the similarity, we have
$$
\frac{l}{x}=\frac{x}{l-x}
$$
so
$$
l^2-lx=x^2
$$
and, easily,
$$
x=\frac{\sqrt{5}-1}{2}l
$$
(the negative root must be discarded, of course). Thus
$$
\cos\frac{2\pi}{5}=\frac{\sqrt{5}-1}{4}
$$
and it's easy to compute $\sin(\pi/5)$ and $\cos(\pi/5)$ from this.
One can use the outlined strategy, too. The key is using $\pi/10$ and not $x=\pi/5$. If $x=\pi/10$, then
$$
\frac{\pi}{2}-3x=\frac{5\pi}{10}-\frac{3\pi}{10}=\frac{2\pi}{10}=2x
$$
and therefore
$$
\tan3x=\tan\left(\frac{\pi}{2}-2x\right)=\cot2x=\frac{1}{\tan2x}
$$
Now we can apply the formulas and get
$$
\frac{3\tan x-\tan^3x}{1-3\tan^2x}=\frac{1-\tan^2x}{2\tan x}
$$
or, setting $t=\tan x$,
$$
6t^2-2t^4=1-3t^2-t^2+3t^4
$$
that reduces to
$$
5t^4-10t^2+1=0
$$
This gives
$$
t^2=\frac{5+2\sqrt{5}}{5}
$$
But $\tan(\pi/5)=\tan2x$ or
$$
\tan\frac{\pi}{5}=\frac{2t}{1-t^2}
$$
and just substituting will give the result.