Please explain this explanation to me; Discrete Math: Counting

Question

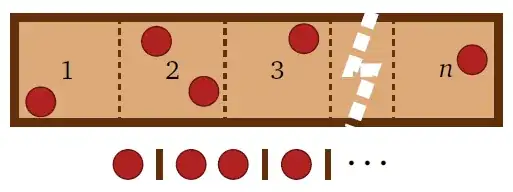
This is a counting solution to which selections of object which are not all distinct.

The basic premise is that the number of non-negative integer solutions to $x_1+x_2+x_3+...+x_k = n$ is equal to the number of ways to place $n$ identical balls into $k$ labelled boxes in which is equal to the number of sequences of $n$ stars (*) and $k-1$ bars (|).

The correspondence in the former case is to let $x_i$ equal the number of balls in box $i$, $1 \leq i \leq k$, and in the latter case it is to let the number of stars before the first bar equal the number of balls in box $1$, the number of stars between the first and second bar equal the number of balls in box $2$, the number of stars between the second and third bar equal the number of balls in box $3$, and so on until, finally, the number of stars following the last bar equals the number of balls in box $k$.

You can imagine the $n$ stars as the balls, and the $k$ spaces created by the $k-1$ bars as the $k$ boxes. The number of solutions is then the number of arrangements of these $n+k-1$ non distinct objects, and is $$\frac{(n+k-1)!}{n!(k-1)!} = C(n+k-1, n) = C(n+k-1, k-1).$$

Any explanation would be appreciated

Answer 1

It is a way to describe the number of ways you can choose $k$ objects out of $n$ without regard to order and with replacement.

First, imagine an experiment where we have a box with $n$ compartments. We draw a number between $1$ and $n$ from an urn, place a ball in the corresponding compartment, and put the number back in the urn. This is repeated $k$ times, which gives some configuration of the box:

As indicated in the figure, this configuration is equivalent to a sequence of $k$ red balls and $(n-1)$ inner walls, i.e. the walls separating the compartments. It is possible to construct $(n-1+k)!$ such sequences (with regard to order). But since we only care about the number of balls in each compartment, some of these sequences are identical. Swapping two balls in the sequence, will not change the configuration of the box, and the total number of ways to permute the balls is $k!$. Likewise, the inner walls can be permuted in $(n-1)!$ ways. This gives \begin{align*} \frac{(n-1+k)!}{(n-1)!k!}=\binom{n-1+k}{k} \end{align*} possible ways to choose $k$ out of $n$ objects without regard to order and with replacement.

In respect to the problem $x_1+\ldots+x_n=k$, this is exactly the same problem as placing the balls in the compartments. Think of $x_1$ as the number of balls in compartment 1, $x_2$ the number in compartment 2 etc. In total, there are $k$ balls, which gives the equation.