$\sin 1^\circ$ is irrational but how do I prove it in a slick way? And $\tan(1^\circ)$ is .....

Question

In the book 101 problems in Trigonometry, Prof. Titu Andreescu and Prof. Feng asks for the proof the fact that $\cos 1^\circ$ is irrational and he proves it. The proof proceeds by contradiction and using the strong induction principle. (Problem on Pg:84, 70 in typeset; solution on Pg:126, 111 in Typeset). However, for Completeness, I'll append it here:

Proof of irrationality of $\cos (1^\circ)$

Assume for the sake of contradiction, that $\cos(1^\circ)$ is rational. Since, $$\cos(2^\circ)=2\cos^2(1^\circ)-1$$ we have that, $\cos(2^\circ)$ is also rational. Note that, we also have $$\cos(n^\circ +1 ^\circ)+\cos(n^\circ -1 ^\circ)=2\cos(1^\circ)\cdot \cos(n^\circ)$$ By Strong induction principle, this shows that $\cos(n^\circ)$ is rational for all integers $n \geq 1$. But, this is clearly false, as for instance, $\cos(30^\circ)=\dfrac{\sqrt{3}}{2}$ is irrational, reaching a contradiction.

But, as my title suggests, $\sin(1^\circ)$ is irrational, (look at the following image for its value!)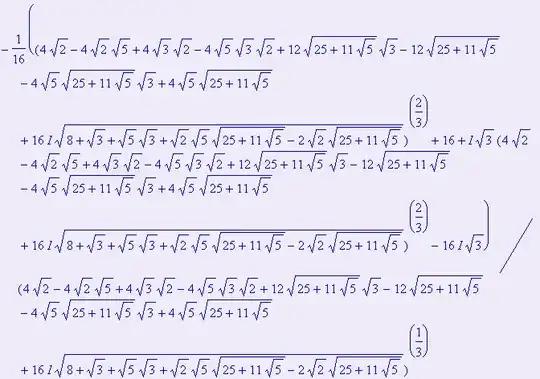

Is there a proof as short as the above proof or can any of you help me with a proof that bypasses actual evaluation of the above value?

Image Courtesy: http://www.efnet-math.org/Meta/sine1.htm This link explains how to evaluate this value.

My next question is

Is $\tan(1^\circ)$ rational and is there a short proof that asserts or refutes its rationality?

P.S.: This is not a homework question.

Answer 1

If it's a slick proof you want, nothing beats this proof that the only cases where both $r$ and $\cos(r \pi)$ are rational are where $\cos(r \pi)$ is $-1$, $-1/2$, $0$, $1/2$ or $1$.

If $r=m/n$ is rational, $e^{i \pi r}$ and $e^{-i \pi r}$ are roots of $z^{2n} - 1$, so they are algebraic integers. Therefore $2 \cos(r \pi) = e^{i \pi r} + e^{-i \pi r}$ is an algebraic integer. But the only algebraic integers that are rational numbers are the ordinary integers. So $2 \cos(r \pi)$ must be an integer, and of course the only integers in the interval $[-2,2]$ are $-2,-1,0,1,2$.

Answer 2

$\sin(1^\circ) = \cos(89^\circ)$, and since 89 is relatively prime to 360, the proof for $\cos 1^\circ$ works with almost no change.

More precisely: Assume that $\cos(89^\circ)$ is rational. Then, by the same induction as before with every $1^\circ$ replaced by $89^\circ$ we get that $\cos(89n^\circ)$ is rational for every $n\in\mathbb N$. In particular, since $150\times 89=37\times 360+30$, we get that $$\cos(150\times 89^\circ)=\cos(37\times 360^\circ+30^\circ)=\cos(30^\circ)$$ is rational, a contradiction.

For $\tan(1^\circ)$, a slight variant of the same proof works. Assume that $\alpha = \tan(1^\circ)$ is rational. Then $1+\alpha i$ is in $\mathbb Q[i]$, and then $\tan(n^\circ)$, being the ratio between the imaginary and real parts of $(1+\alpha i)^n$ is also rational. But $\tan(30^\circ)$ is not rational, so $\tan(1^\circ)$ cannot be either.

Answer 3

You can prove it exactly the same way:

Assume by contradiction that $\sin(1^\circ)$ is rational.

Then

$$\cos(2^\circ)=1- 2\sin^2(1^\circ) \mbox{is rational}\,,$$

Now you can also prove that $\cos 4^\circ$ is rational.

Using

$$\cos((2n+2)^\circ)+\cos((2n-2) ^\circ)=2\cos(2^\circ)\cdot \cos((2n)^\circ) \,,$$

you can prove by induction that $\cos(2n^\circ)$ is rational, and you get your contradiction...

Added

If $\tan(1^\circ)$ is rational, then

$$\cos(2^\circ) =\frac{1- \tan^2(1^\circ)}{1+\tan^2(1^\circ)}$$ is also rational...

Alternately, if you are not familiar with this relation, note that

$$\cos^2(1^\circ)= \frac{1}{\sec^2(1^\circ)}= \frac{1}{1+ \tan^2(1^\circ)}$$ is rational, thus

$$\cos(2^\circ)=2\cos^2(1^\circ)-1$$ is rational.

The first part of the proof finishes this part too...

P.S. You can actually prove by induction the following result: if $\cos(x)$ is rational, then $\cos(nx)$ is also rational.

Answer 4

Interestingly enough,I happened to encounter this very problem (regarding $\tan 1^\circ$) yesterday.

Let's assume $\tan 1^\circ$ is rational.Then we can repeatedly use the formula $\tan (A+B)=\frac{\tan A+ \tan B}{1- \tan A \tan B}$ to get that $\tan 60^\circ = \sqrt{3}$ is rational as well, a contradiction.

Answer 5

(Too long for a comment.)

Jack Calcut's article gives the following result:

Corollary: The only rational values of $\tan\,k\pi/n$ are $0$ and $\pm1$.

which rests on the lemma

Main Lemma: Let $z\neq0$ be a Gaussian integer. There is a natural number $n$ such that $z^n$ is real iff either $\Re z=0$, $\Im z=0$, $\Re z=\Im z$, or $\Re z=-\Im z$.

If $\tan\dfrac{k\pi}{n}=\dfrac{q}{p}$, then $\dfrac{k\pi}{n}=\arg(p+iq)$, and $k\pi=\arg((p+iq)^n)$, which implies $(p+iq)^n$ is an integer. If $(p+iq)^n$ is an integer, then $\dfrac{k\pi}{n}$ is an integer multiple of $\pi/4$ by the Main Lemma. Since $\tan$ is $\pi$-periodic, $\tan\,0=0$, and $\tan\dfrac{\pm \pi}{4}=\pm 1$, the corollary is established.

---

For giggles, I asked Mathematica for the following explicit radical representations:

$$\begin{split}\sin\frac{\pi}{180}=-\frac1{\sqrt[3]{2}}\left(\frac1{32}+\frac{i}{32}\right)&\left(\sqrt[3]{-1-i\sqrt{3}} \left(1-i\sqrt{3}\right)\left(\sqrt{2}+\sqrt{10}-2i\sqrt{5-\sqrt{5}}\right)+\right.\\&\left.\sqrt[3]{-1+i\sqrt{3}}\left(\sqrt{3}-i\right)\left(\sqrt{2}+\sqrt{10}+2i\sqrt{5-\sqrt{5}}\right)\right)\end{split}$$

$$\scriptsize \tan\frac{\pi}{180}=-\frac{\sqrt[3]{-1-i \sqrt{3}} \left(1-i \sqrt{3}\right) \left(\sqrt{2}+\sqrt{10}-2i\sqrt{5-\sqrt{5}}\right)+\sqrt[3]{-1+i\sqrt{3}} \left(\sqrt{3}-i\right)\left(\sqrt{2}+\sqrt{10}+2i\sqrt{5-\sqrt{5}}\right)}{\sqrt[3]{-1-i\sqrt{3}}\left(\sqrt{3}+i\right) \left(\sqrt{2}+\sqrt{10}-2i\sqrt{5-\sqrt{5}}\right)+\sqrt[3]{-1+i\sqrt{3}}\left(\sqrt{3}-i\right) \left(2 \sqrt{5-\sqrt{5}}-i\left(\sqrt{2}+\sqrt{10}\right)\right)}$$

Answer 6

We have $\sin(5*x)=16*\sin(x)^5-20*\sin(x)^3+5*\sin(x)$ and $\sin(3*x)=3*\sin(x)-4*\sin(x)^3$

Suppose that $\sin(1)$ is rational then according to first relation $\sin(5)$ is rational.Now by using relation $2$ conclude that $\sin(15)$ is rational. repeat this process and by using again of relation two conclude that $\sin(45)$ is rational. We know that it is the half of the root of $2$ and this is a contradiction so $\sin(1)$ is irrational

Answer 7

Note that $\cos(2x) = \frac{1-\tan^2(x)}{1+\tan^2(x)}$. So if $\tan(x)$ is rational, or even the square root of a rational, $\cos(2x)$ must be rational. Combine this with Niven's Theorem to answer the question about $\tan$.