I have an ascending cubic Bézier curve. ($x_0 \leq x_1 \leq x_2 \leq x_3$) Considering this property, there is always one and only one $y$ value per $x$ value.
The point ($x, y$) along the curve is determined by the following equation, from Wikipedia:
$B(t) = (1-t)^3 P_0 + 3t (1-t)^2 P_1 + 3t^2 (1-t) P_2 + t^3 P_3$
However, this equation takes $t$ as a parameter, which is the progression along the curve, or, as Wikipedia explains,
The $t$ in the function for a linear Bézier curve can be thought of as describing how far $B(t)$ is from $P_0$ to $P_n$. For example when $t=0.25$, $B(t)$ is one quarter of the way from point $P_0$ to $P_n$.
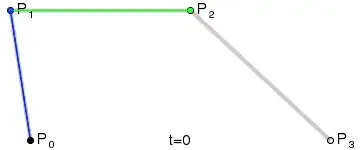
I would like to use the $B(t)$ function with a $x$ parameter instead. Something like $B(x)$, or anything that can convert a given $x$ to a $t$.
Edit: I realized that I could solve $B(t)$ for $t$:
$B(t) = (1-t)^3 P_0 + 3t (1-t)^2 P_1 + 3t^2 (1-t) P_2 + t^3 P_3$
$x(t) = (1-t)^3 x_0 + 3t (1-t)^2 x_1 + 3t^2 (1-t) x_2 + t^3 x_3$
$x(t) = (-x_0+3x_1-3x_2+x_3)t^3 + (3x_0-6x_1+3x_2)t^2 + (-3x_0+3x_1)t + x_0$
$t(x) = ...?$
Edit 2: With the Newton-Raphson method, I managed to reach my goal. I'm attaching a screenshot.
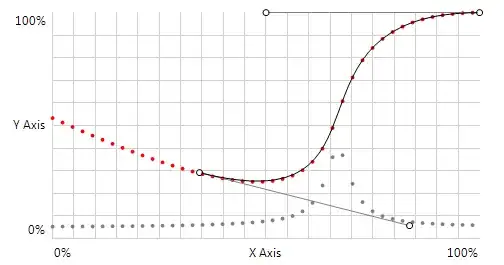
The red dots represent my interpolation (and surprisingly, extrapolation as well. This was an unexpected but great surprise!).
The gray dots represent a small optimization I made to the method: the number of iterations based on the difficulty to approximate. I increase the precision in an invertly proportional relation to the absolute value of the derivative: $$p\ \alpha\ \frac{1}{|B'(t_n)|}$$
I have to tweak the parameters, but so far, this method is efficient and pretty safe, even at a nearly straight slope. Thanks for the help!
P.S.: The more explicit solution, without the precision adjustment (which is unfortunately only well represented in procedural code):
$$t\approx x-\sum_{n=0}^p (\frac{B(t)_x-x}{B'(t)_x})$$
(This takes advantage of the fact that $-x$ is nullified in the derivative Also note that $t$ is reassigned at each step of the sum).
P.P.S.: The accompanying code:
p = 5;
p_max = 100;
t = x;
for (n = 0; n < min(p, p_max); n++)
{
d = dB(t).x;
if (p < p_max) p += min(0.02 / d^2), 1);
t -= (B(t).x - x) / d;
}
return t;