Geometric interpretation of mixed partial derivatives?

Question

I'm looking for a geometric interpretation of this theorem:

My book doesn't give any kind of explanation of it. Again, I'm not looking for a proof - I'm looking for a geometric interpretation.

Thanks.

Answer 1

Inspired by Ted Shifrin's comment, here's an attempt at an intuitive viewpoint. I'm not sure how much this counts as a "geometric interpretation".

Consider a tiny square $ABCD$ of side length $h$, with $AB$ along the $x$-axis and $AD$ along the $y$-axis.

D---C
|   | h
A---B
  h

Then $f_x(A)$ is approximately $\frac1h\big(f(B)-f(A)\big)$, and $f_x(D)$ is approximately $\frac1h\big(f(C)-f(D)\big)$. So, assuming by $f_{xy}$ we mean $\frac\partial{\partial y}\frac\partial{\partial x}f$, we have $$f_{xy}\approx\frac1h\big(f_x(D)-f_x(A)\big)\approx\frac1{h^2}\Big(\big(f(C)-f(D)\big)-\big(f(B)-f(A)\big)\Big).$$ Similarly, $$f_{yx}\approx\frac1{h^2}\Big(\big(f(C)-f(B)\big)-\big(f(D)-f(A)\big)\Big).$$ But those two things are the same: they both correspond to the "stencil" $$\frac1{h^2}\begin{bmatrix} -1 & +1\\ +1 & -1 \end{bmatrix}.$$

Answer 2

One thing to think about is that the derivative in one dimension describes tangent lines. That is, $f'$ is the function such that the following line, parametrized in $x$, is tangent to $f$ at $x_0$: $$y(x)=f(x_0)+f'(x_0)(x-x_0).$$ We could, in fact, go further, and define the derivative to be the linear function which most closely approximates $f$ near $x_0$. If we want to be really formal about it, we could say a function $y_0$ is a better approximation to $f$ near $x$ than $y_1$ if there exists some open interval around $x$ such that $|y_0(a)-f(a)|\leq |y_1(a)-f(a)|$ for every $a$ in the interval. The limit definition of the derivative ensures that the closest function under this definition is the $y(x)$ given above and it can be shown that my definition is equivalent to the limit definition.

I only go through that formality so that we could define the second derivative to be the value such that $$y(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{1}2f''(x_0)(x-x_0)^2$$ is the parabola which best approximates $f$ near $x_0$. This can be checked rigorously, if one desires.

However, though the idea of the first derivative has an obvious extension to higher dimensions - i.e. what plane best approximates $f$ near $x_0$, it is not as obvious what a second derivative is supposed to represent. Clearly, it should somehow represent a quadratic function, except in two dimensions. The most sensible way I can think to define a quadratic function in higher dimension is to say that $z(x,y)$ is "quadratic" only when, for any $\alpha$, $\beta$, $x_0$ and $y_0$, the function of one variable $$t\mapsto z(\alpha t+x_0,\beta t+y_0)$$ is quadratic; that is, if we traverse $z$ across any line, it looks like a quadratic. The nice thing about this approach is that it can be done in a coordinate-free way. Essentially, we are talking about the best paraboloid or hyperbolic paraboloid approximation to $f$ as being the second-derivative. It is simple enough to show that any such function must be a sum of coefficients of $1$, $x$, $y$, $x^2$, $y^2$, and importantly, $xy$. We need the coefficients of $xy$ in order to ensure that functions like $$z(x,y)=(x+y)^2=x^2+y^2+2xy$$ can be represented, as such functions should clearly be included our new definition quadratic, but can't be written just as a sum of $x^2$ and $y^2$ and lower order terms.

However, we don't typically define the derivative to be a function, and here we have done just that. This isn't a problem in one dimension, because there's only the coefficient of $x^2$ to worry about, but in two-dimensions, we have coefficients of three things - $x^2$, $xy$, and $y^2$. Happily, though, we have values $f_{xx}$, $f_{xy}$ and $f_{yy}$ to deal with the fact that these three terms exists. So, we can define a whole ton of derivatives when we say that the best approximating quadratic function must be the map $$z(x,y)=f(x,y)+f_x(x,y)(x-x_0)+f_y(x,y)(y-y_0)+\frac{1}2f_{xx}(x,y)(x-x_0)^2+f_{xy}(x,y)(x-x_0)(y-y_0)+\frac{1}2f_{yy}(x,y)(y-y_0)^2$$ There are two things to note here:

Firstly, that this is a well-defined notion regardless of whether we name the coefficients or arguments. The set of quadratic functions of two variables is well defined, regardless of how it can be written in a given form. Intuitively, this means that, given just the graph of the function, we can draw the surface based on local geometric properties of the graph of $f$. The existence of the surface is implied by the requirement that $f_{xy}$ and $f_{yx}$ be continuous.

Secondly, that there are multiple ways to express the same function; we would expect that it does not matter if we use the term $f_{xy}(x,y)(x-x_0)(y-y_0)$ or $f_{yx}(x,y)(y-y_0)(x-x_0)$ because they should both describe the same feature of the the surface - abstractly, they both give what the coefficient of $(x-x_0)(y-y_0)$ is for the given surface, and since the surface is well-defined without reference to derivatives, there is a definitive answer to what the coefficient of $(x-x_0)(y-y_0)$ is - and if both $f_{xy}$ and $f_{yx}$ are to answer it, they'd better be equal. (In particular, notice that $z(x,y)=xy$ is a hyperbolic paraboloid, which is zero on the $x$ and $y$ axes; the coefficient of $(x-x_0)(y-y_0)$ can be thought of, roughly as a measure of how much the function "twists" about those axes, representing a change that affects neither axis, but does affect other points)

Answer 3

Here's the best way I've found to think of it.

First, the background material:

Take a function $f(x,y)$.

$f_x$ = the partial derivative measuring the rate of change (the slope) of $f$ in the $x$-direction.

$f_y$ = the partial derivative measuring the rate of change (the slope) of $f$ in the $y$-direction.

$f_{xx}$ = the rate of change of $f_x$ as one moves in the $x$-direction. Similar to the second derivative for a one-variable function, it shows if the slope is increasing (concave up) or decreasing (concave down).

Now, the mixed part:

$f_{xy}$ = the mixed partial derivative measuring the rate of change of the slope in the $x$-direction as one moves in the $y$-direction.

$f_{yx}$ = the mixed partial derivative measuring the rate of change of the slope in the $y$-direction as one moves in the $x$-direction.

The original poster's theorem says that these mixed partial derivatives are equal (given appropriate function behavior): $f_{xy}=f_{yx}$

Here's my reference with a nice figure: https://legacy-www.math.harvard.edu/archive/21a_fall_08/exhibits/fxy/index.html

---

SUPPLEMENT:

• For consistency, I've used the idea from Ted Shifrin's comment and Rahul's answer/figure. I've included some colorized figures, which might help with the geometric interpretation for some individuals.

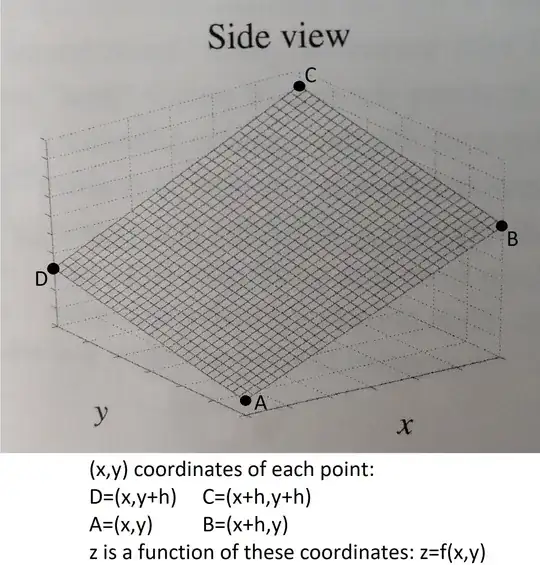
Perhaps, a good way to think of the equality of mixed partial derivatives is like this: the change in slope (in the y-direction) of the changes in slope (in the x-direction) is the same as the change in slope (in the x-direction) of the changes in slope (in the y-direction). Either way, we're effectively finding the change in slope between the high point(C) and the low point (A), with consideration to the intervening points (B and D), for the particular function we're working with. Whether we go via the x-direction first or the y-direction first doesn't matter.

Answer 4

I shall try to explain understanding gained from mechanics of materials or applied mechanics.As far as geometrical interpretation goes, there is nothing more visible than twist in a twisted plate or strip quantifying the mixed partial derivative.

$f_{xx}$ is normal curvature in reference direction and $f_{xy} $ is the torsion in the reference direction for a function.It is rate of change of x-tangential rotation translated with respect to y direction.

At the level of the differential lengths ( in a sketch made with finite differences) along x- and y-, if $f_{xy}$ is different from $ f_{yx}$ then the points opposite the differential quadrilateral do not meet, and it would not be a closed curve!

Hypar Mixed Derv SE

For a surface Z= f(x,y).. $Z_{xx}$ are normal curvatures $Z_{xy}$ is geodesic torsion of line on surface in reference direction .

In the the chart above a hyperbolic paraboloid example is given.The same surface is rotated to obtain different equational forms, to study curvatures in a fixed (x-axis) reference.

Geometrically interpreted normal Curvatures are well known and recognized as $Z_{xx}, Z_{yy} $.

Torsion of line $Z_{xy}$ is cross derivative.It is also referred to as Twist curvature.

Note that the torsion of asymptotes in the example have opposite sense as sign changes from 2 to -2 for surface z = 2 x y changing to -2 x y.Principal directions of surface have no torsion. The diagonal lines have maximum torsion with maximum value of mixed derivative.

To understand torsion in relation to curvature and torsion of surface lines ( not one dimensional lines in 3-space) the Mohr’s Circle is most instructive.

Euler’s Formula and geodesic Torsion formula must be mentioned (perhaps taught) together as component properties of a single physical surface line just as we have the mathematical sense of straight and mixed derivatives together.

Stress,strain, curvature, moment of inertia are in fact tensors , one direction is for reference and another for applied force.

If $ k_1$ and $k_2$ are principal curvatures at any point and angle TMA = $ 2 \psi$,

Normal curvature $ k_n = k_1 \cos^2 \psi + k_2 \sin^2 \psi$ and Geodesic Torsion $ \tau_g = (k_1-k_2)\sin\psi \cos\psi $

The first is Euler Formula in surface theory that should be followed by geodesic torsion in its mentioning.

EDIT: Relates to geometry and rigidity in structural design.

1. Moebius strip is example of twisting effect / mixed derivative.( non-orientability is not the point here.)

2. Ruled surfaces necessarily have negative Gauss curvature consequential to such twistings.

3. Tacoma Narrows bridge disaster: Structural Engineers have been and even now continue to ignore the importance of mixed derivative in design.

TacomaNarrowsTwistDisaster

4. In composite materials laminate design one places reinforcements in 45 degrees also, to impart rigidity after catering to main $ z_{xx}$ curvature.

Answer 5

Ok, this is very crude and definitely not a proof. I wanted to post it as a comment but I don't have the reputation.

If you think of $f_x$ as "taking a step" in the direction of increasing $x$ and seeing how much $f$ has changed, you could think of $f_{xy}$ as taking a step in the $x$ direction first and in the $y$ direction next, and of $f_{yx}$ as taking the same steps in the opposite order.

The unsatisfactory part is that $f_{xx}$ and $f_{yy}$ are hard to interpret as "taking two steps" in the $x$ or $y$ directions, but possibly a satisfactory definition of "step" can be conjured up.

Answer 6

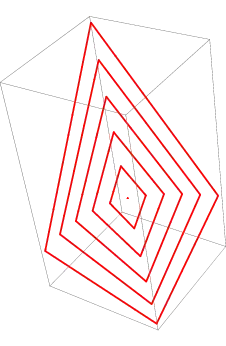
Example of a regular function (graph in blue) and the image of a square (in red) for different lengths (see Rahul's answer):

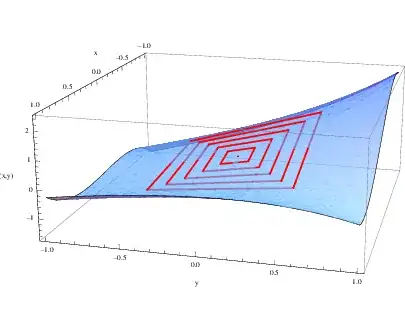
Same picture without the graph of $f$: the opposite segments become parallel when the step decreases. This is a geometric interpretation of Schwarz theorem.