How do I verify this fact, measure theory?

Question

This is from my book:

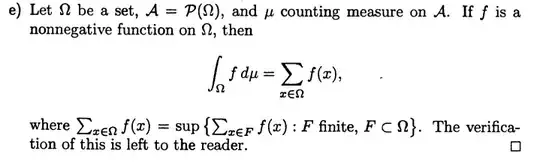
As you see it is up to me to verify it for myself. But I do not know how?

I know that the integral of f is defined to be:

$\int f d\mu=\sup\{\int sd\mu | \text{s simple,} s \le f\}=\sup\{\int\Sigma a_i*X_{A_i} d\mu| \text{s simple,} s \le f\}$

$=\sup\{\Sigma a_i*\mu(A_i)| \text{s simple,} s \le f\}$

$=\sup\{\Sigma a_i*N(A_i)| \text{s simple,} s \le f\}$

I need to show that this last expression is equal to the expression given in the comment in the book. From what I see, the expression given in the book is also a sup over simple function, so I know that my expression must be bigger or equal to the expression in the book?, is this correct? But if so, what about the other way?

Answer 1

I can show it under the assumption that $\Omega$ is countable. Let $F_i$, $i\geq 1$, be an increasing sequence of finite subsets of $\Omega$ such that $\cup_{i\geq1}F_i=\Omega$. We can then consider the following sequence of $\cal A$-measurable nonnegative functions for $n\geq 1$: $$ f_n(\omega) = \sum_{x \in F_n}f(x)1_{\{x\}}(\omega). $$ This sequence is increasing and converges pointwise to $f$. Note also that: $$ \int_\Omega f_n d\mu =\sum_{x \in F_n}f(x)\mu(\{x\})=\sum_{x \in F_n}f(x).$$ Then by monotone convergence theorem we get: $$ \int_\Omega f d\mu = \lim_{n\to \infty }\int_\Omega f_n d\mu = \lim_{n\to \infty }\sum_{x \in F_n}f(x) =:\sum_{x\in \Omega}f(x).$$