Why Doesn't This Series Converge?

Question

I am teaching a Calc II course and came across the following series when finding the interval of convergence for the Taylor series of $f(x)=\sqrt{x}$ centered at $x=1$:

$$ \sum_{n=2}^\infty \frac{1\cdot 3\cdot 5\cdot 7\cdots (2n-3)}{2^nn!}. $$

I know that it doesn't converge, but how do you show it? I would like to be able to use only the technology of a Calc II course, but any answer would be enlightening.

Edit: I probably should mention that the reason I did not think it converged was Wikipedia said so. After the wonderful answers below, I fixed it. Beware of Wikipedia. And thanks MathStacks!

Answer 1

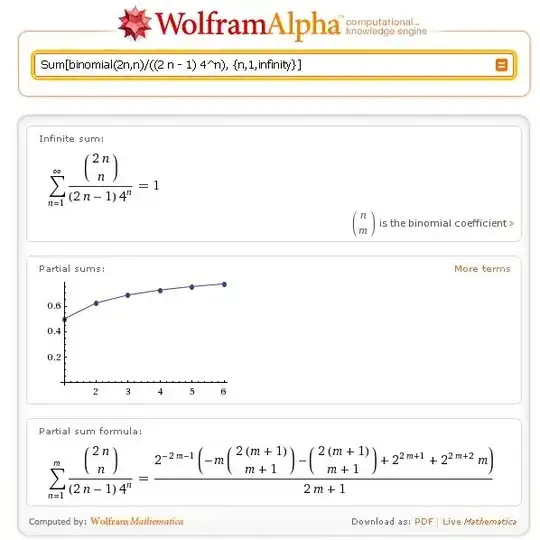
I don't think the series diverges.

$$ \frac{1 \cdot 3 \cdot 7 \cdots (2n-3)}{2 \cdot 4 \cdot 6 \cdots 2n}$$

$$ = \frac{{2n \choose n}}{(2n-1)4^n} = \frac{1}{(2n-1)\sqrt{\pi n}}(1 + O(\frac{1}{n}))$$

using the approximation

$$\frac{ {2n \choose n}}{4^n} = \frac{1}{\sqrt{\pi n}}(1 + O(\frac{1}{n}))$$

and so the series must converge! Perhaps you have a mistake in your computation?

For a more elementary proof of convergence, see the end of the answer.

I believe you should be able to compute it using the series expansion for

$$\frac{1}{\sqrt{1-x^2}} = \sum_{k=0}^{\infty} \frac{{2k \choose k} x^{2k}}{4^k}$$

(you will need to subtract some terms, divide by $x^2$ and integrate).

---

An elementary proof of convergence.

We will show that

if $\displaystyle S_n = \frac{1 \cdot 3 \cdots (2n-1)}{2 \cdot 4 \cdots 2n}$ then $\displaystyle S_n \le \frac{1}{\sqrt{n+1}}$

This proves the partial term of your series, which is $\displaystyle \sum_{k=2}^{n} \frac{S_k}{2k-1} < \sum_{k=2}^{\infty} \frac{1}{(2k-1)\sqrt{k+1}} < C$ (for some constant $C$), and thus is bounded above. Since the series is monotonically increasing and bounded above, it is convergent.

We will prove that $\displaystyle S_n \le \frac{1}{\sqrt{n+1}}$ by induction on $n$.

For $n=1$ it is clearly true.

Now $S_{n+1} = S_n \frac{2n+1}{2n+2}$

Consider $\displaystyle 1 - \frac{2n+1}{2n+2} = \frac{1}{2n+2} \ge \frac{1}{\sqrt{n+2}(\sqrt{n+2} + \sqrt{n+1})} = \frac{\sqrt{n+2} - \sqrt{n+1}}{\sqrt{n+2}}$

Thus $\displaystyle \frac{2n+1}{2n+2} \le \frac{\sqrt{n+1}}{\sqrt{n+2}}$ and so

$\displaystyle S_{n} \le \frac{1}{\sqrt{n+1}} \Rightarrow S_{n+1} \le \frac{1}{\sqrt{n+2}}$

Answer 2

You can use Taylor approximations here. Note that the ratio between consecutive terms is ${2n - 3 \over 2n} = \exp(\ln(1 - 3/2n)) = \exp(-{3 \over 2n} + O(1/n^2))$. So the product is comparable to $\exp(-{3 \over 2} \sum_{i = 2}^n {1 \over n} + O(1/n))$, which in turn is comparable to $\exp(-{3 \over 2} \ln(n))$ or $n^{-{3 \over 2}}$. Thus the series converges.

Comment: Seeing others computing the actual value... once you know it converges (absolutely) you can use the original power series to get the actual value. For $|x| < 1$, $(1 - x)^{1 \over 2} = 1 - {x \over 2} - {1 \over 2} \sum_{n=2}^{\infty} A_nx^n$, where $A_n$ is the $n$ term of the sum. Since all terms of the sum are positive and it converges for $x = 1$, if you take limits as $x$ goes to 1 you get the sum $S$ we're looking at. In other words, 0 = 1 - 1/2 - ${S \over 2}$ or $S = 1$.

And actually if you think about it.. if the series did diverge, taking limits of the series as $x$ goes to 1 from below would give infinity since all terms are positive. Thus just taking limits of both sides as $x$ goes to 1 gives both convergence and the correct value.

Answer 3

Further to the other answers posted, not only does the sum converge, but you can conclude that it converges precisely because of the way it was derived. As you state, the terms $C_n=\frac{1\cdot3\cdot5\cdot7\cdots(2n-3)}{2^nn!}$ arise as the Taylor expansion of $f(x)=\sqrt{x}$ about $x=1$, $$ \sqrt{1-x}=1-\frac{x}{2}-\sum_{n=2}^\infty C_nx^n. $$ As $\sqrt{1-x}$ is a well-defined analytic function for $\Vert x\Vert < 1$, this has radius of convergence 1. Also, as the square root is well defined at 0, monotone convergence gives $$ \sum_{n=2}^\infty C_n=\lim_{x\to1}\sum_{n=2}^\infty C_nx^n=\lim_{x\to1}\left(1-\frac{x}{2}-\sqrt{1-x}\right)=\frac12. $$

Answer 4

Let's start with the formula

$\displaystyle \sum_{n=1}^\infty \frac{\binom{2n}{n}}{(2n-1)4^n}.$

Note that

$\displaystyle \frac{\binom{2n}{n}}{2n-1} = \frac{(2n)!}{(2n-1)n!n!} = 2 \frac{(2n-2)!}{n!(n-1)!} = 2C_{n-1},$

where $C_n$ is the $n$th Catalan number.

Now $C_n$ counts the number of paths of length $2(n+1)$ that reach the origin for the first time at their end, always being to the right of the origin.

Since a one-dimensional random walk will get back to the origin w.p. $1$,

$\displaystyle \sum_{n=1}^\infty \frac{C_{n-1}}{4^n} = \frac{1}{2}.$

Therefore the original sum equals

$\displaystyle \sum_{n=1}^\infty \frac{2C_{n-1}}{4^n} = 1.$

Answer 5

Using Stirling formula $n!\sim \sqrt {2\pi n}(n/e)^n$, I also get that the $n$th term of the series is $O(1/n^{3/2})$. So the series is convergent. In the derivation I used that $$\lim_{n\to\infty}\left(1-\frac{1}{n}\right)^n=e^{-1}.$$

Answer 6

In fact the sum converges. You can find a closed form by massaging the formula that I posted on Hadamard products viz. $\rm\ (1-4x)^{-1/2} \;=\; \sum\ \binom{2n}{n}\ x^n\:.\ $ See also this post. Alternatively:

Answer 7

The series ${ \sum _{2} ^{\infty} \frac{1 \cdot 3 \cdot 5 \cdot \ldots \cdot (2n-3) }{2 ^n n!} }$ is ${ \sum _{2} ^{\infty} \vert \binom{1/2}{n} \vert }.$

Because ${ \vert \binom{1/2}{n} \vert }$ ${ = \frac{1}{n!} \vert \prod _{0} ^{n-1} (\frac{1}{2} - j) \vert }$ ${ = \frac{1}{n!} \left( \frac{\prod _{1} ^{n-1} (2j-1)}{2 ^n} \right) }$ for ${ n \geq 2 }.$

It converges, and infact :

Th: Let ${ \alpha \gt 0 }.$ Then ${ \sum _{1} ^{\infty} \vert \binom{\alpha}{n} \vert }$ converges.
Pf: When ${ \alpha }$ is a positive integer this holds trivially, so suppose ${ \alpha }$ is positive but not an integer. Now ${ a _n := \vert \binom{\alpha}{n} \vert }$ ${ \gt 0 }.$ Also ${ \frac{a _{n+1}}{a _n} }$ ${ = \vert \frac{\alpha - n}{n+1} \vert }$ ${ = \frac{n-\alpha}{n+1} }$ whenever ${ n \geq \alpha }.$ That is, ${ n a _n - (n+1) a _{n+1} }$ ${ = \alpha a _n }$ whenever ${ n \geq A := \lceil \alpha \rceil }.$
So ${ \alpha (\sum _{A \leq n \leq N} a _n ) }$ ${ = \sum _{A \leq n \leq N} (n a _n - (n+1) a _{n+1}) }$ ${ = A a _A - (N+1) a _{N+1} }$ ${ \leq A a _A }$ for arbitrary ${ N \geq A }.$ So the partial sums of ${ \sum _{1} ^{\infty} a _n }$ are bounded above and hence convergent.