2

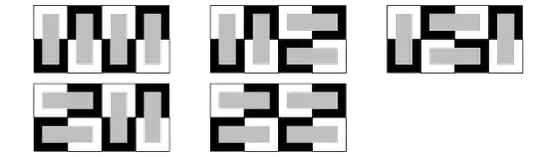
There is a remarkable relation between Fibonacci numbers and its squares:

$F^{2}_{n} +F^{2}_{n+1}=F_{2n+1}$.

I know how to prove it using $F_{n}=\frac{\sqrt{5}}{5}((\frac{1+\sqrt{5}}{2})^n -(\frac{1-\sqrt{5}}{2})^n)$ formula, but I want a proof without this. By proof I don't mean a rigid one. I tried to use area of rectangles but no success! Also, I saw some proof by induction but it is not my point - I want a proof using picture and not rigid, that I hope I could explain well!

VividD
  • 15,966
kpax
  • 2,911

2 Answers2

4

The identity from the question can be viewed in a completely different way.

First, Fibonacci number of order n can be defined as number of ways for 2×1 dominoes to cover a 2×n checkerboard:

n=3:

enter image description here

n=4:

enter image description here

n=5:

enter image description here

Then, one can use methods presented in this paper to prove the original identity.

There is another MSE question here, that makes use of tiling, but with different tiles, and proves identity:

$$n F_1 + (n-1)F_2 + \cdots + F_n = F_{n+4} - n - 3$$

Community
  • 1
VividD
  • 15,966
3

This relation is particular case of Catalan's Identity: $$ F_n^2 - F_{n+r}F_{n-r} = (-1)^{n-r}F_r^2 $$ With $r = n+1 $ we have $$ F_n^2 - F_{2n+1}F_{1} = (-1)^{2n-1}F_{n+1}^2 \Rightarrow F_n^2 + F_{n+1}^2 = F_{2n+1} $$

(Refer to Wikipedia )

Nick
  • 6,804
Lamberto Lamberti
  • 315