Evaluating a series to order "three halves"

Question

In doing some calculations related to one-dimensional Brownian Motion confined to a finite interval, I have come across functions such as

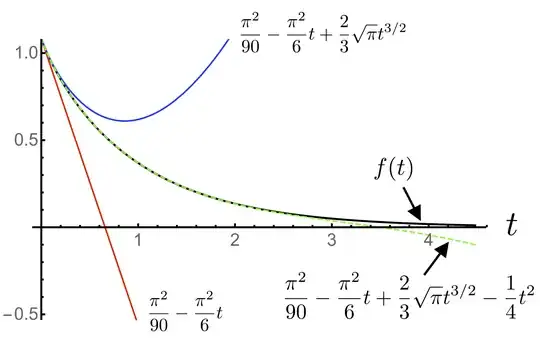
$$ f(t) = \sum_{n=1}^\infty\frac{\exp(-n^2t)}{n^4}. $$ I am interested in the behavior of this function for small $t$. By expanding the exponential it is easy to get the terms of order 0 and 1 in $t$. However, the term of order $t^2$ diverges. I take this to mean that $f(t)$ does not have a second derivative at $t = 0$. I think (although I'm not sure) that in some sense there is a "3/2" order term. How does one define and calculate this term? Perhaps the limit $$ \lim_{t \to 0}\frac{f(t) - f(0) - t f'(0)}{t^{3/2}} $$ is finite and can be calculated? Is there an unambiguous way of expanding such functions in power series with fractional powers?

Background: Consider a particle undergoing one-dimensional Brownian Motion in the interval $\left[0,L\right]$ with reflecting boundary conditions. The particle has diffusion coefficient $D$ and its position is $x(t)$. Its initial position is distributed uniformly in the interval. Then one can show that the mean squared displacement at time $t$ is $$ \text{MSD}(t) \equiv \langle \left[x(t) - x(0)\right]^2\rangle = \frac{L^2}{6} + \frac{8 L^2}{\pi^4}\sum_{n=1}^\infty\frac{-1 + (-1)^n}{n^4} \cdot \exp(-t/\tau_n), $$ where $$ \tau_n = \frac{L^2}{n^2 \pi^2 D} $$ As I mentioned, one can calculate this up to first order in $t$. The constant term is of course zero (the particle can't travel any distance in zero time) and the first order term turns out to be $2 D t$, which makes sense since this is the MSD of a free particle (i.e. before it encounters any walls).

Further Notes Here is a plot of the function $f(t)$ given by the series, as well as the approximations from Marko Riedel's answer:

Answer 1

If you start with Taylor expansion $$e^x=\sum_{i=0}^\infty \frac{x^i}{i!}$$ replace $x$ by $-n^2t$ and then $$e^{-n^2t}=1-n^2 t+\frac{n^4 t^2}{2}-\frac{n^6 t^3}{6}+\frac{n^8 t^4}{24}-\frac{n^{10} t^5}{120}+O\left(t^6\right)$$ $$\frac{\exp(-n^2t)}{n^4}=\frac{1}{n^4}-\frac{t}{n^2}+\frac{t^2}{2}-\frac{n^2 t^3}{6}+\frac{n^4 t^4}{24}-\frac{n^6 t^5}{120}+O\left(t^6\right)$$ Summing over $n$ from $1$ to $\infty$ makes a problem with the third and higher terms.

So, in my opinion, if we need more than the first order, we should use $$\sum_{n=1}^\infty\frac{\exp(-n^2t)}{n^4}\sim \frac {\pi^4}{90} -\frac {\pi^2}{6}t+ \alpha t^{\beta}$$ with ($1<\beta<2$) and parameters $\alpha$ and $\beta$ would be adjusted by nonlinear regression for a specified range of $t$.

Based on eleven equally spaced data points ($0\leq t\leq 1$), I obtained $\alpha=0.934254$, $\beta=1.39772$ leading to an $R^2=0.999987$. So the idea, as proposed by Antonio Vargas, of using $\beta=\frac{3}{2}$ seems to be very interesting. Using this last value, I found $\alpha=0.954250$ for $R^2=0.999302$. By the end, why not to simply use $$\sum_{n=1}^\infty\frac{\exp(-n^2t)}{n^4}\sim \frac {\pi^4}{90} -\frac {\pi^2}{6}t+ t^{\frac{3}{2}}$$ which is basically Antonio Vargas's idea and to whom the credit should be given.

Answer 2

It seems to have escaped attention that this sum may be evaluated using harmonic summation techniques which can be an instructive exercise.

Introduce $S(x)%$ given by $$S(x) = \sum_{n\ge 1} \frac{1}{n^4}\exp(-(nx)^2).$$

The sum term is harmonic and may be evaluated by inverting its Mellin transform.

Recall the harmonic sum identity $$\mathfrak{M}\left(\sum_{k\ge 1} \lambda_k g(\mu_k x);s\right) = \left(\sum_{k\ge 1} \frac{\lambda_k}{\mu_k^s} \right) g^*(s)$$ where $g^*(s)$ is the Mellin transform of $g(x).$

In the present case we have $$\lambda_k = \frac{1}{k^4}, \quad \mu_k = k \quad \text{and} \quad g(x) = \exp(-x^2).$$ We need the Mellin transform $g^*(s)$ of $g(x)$, which is

$$\int_0^\infty e^{-x^2} x^{s-1} dx = \int_0^\infty e^{-t} t^{s/2-1/2} \frac{1}{2} t^{-1/2} dt \\ = \frac{1}{2} \int_0^\infty e^{-t} t^{s/2-1} dt = \frac{1}{2} \Gamma(s/2).$$

It follows that the Mellin transform $Q(s)$ of the harmonic sum $S(x)$ is given by

$$Q(s) = \frac{1}{2} \Gamma(s/2) \zeta(s+4) \quad\text{because}\quad \sum_{k\ge 1} \frac{\lambda_k}{\mu_k^s} = \sum_{k\ge 1} \frac{1}{k^4} \frac{1}{k^s} = \zeta(s+4)$$ for $\Re(s) > -3.$

The fundamental strip of the transform of the base function is $\langle 0, \infty \rangle$ and intersecting this with $\langle -3, \infty\rangle$ we obtain that the Mellin inversion integral here is

$$\frac{1}{2\pi i} \int_{1/2-i\infty}^{1/2+i\infty} Q(s)/x^s ds$$ which we evaluate by shifting it to the left for an expansion about zero.

Fortunately the poles of the gamma function term at even integers $\le -6$ are cancelled by the trivial zeros of the zeta function, so that just four poles remain: $s=0, s=-2$ from the gamma function, $s=-3$ from the zeta function and again $s=-4$ from the gamma function.

We have $$\mathrm{Res}\left(Q(s)/x^s; s=0\right) = \frac{1}{2} \times 2 \times \zeta(4) = \frac{\pi^4}{90},$$ and $$\mathrm{Res}\left(Q(s)/x^s; s=-2\right) = \frac{1}{2} \times (-2) \times \zeta(2) \times x^2 = - \frac{\pi^2}{6} x^2,$$ and $$\mathrm{Res}\left(Q(s)/x^s; s=-3\right) = \frac{1}{2} \times \frac{4}{3}\sqrt{\pi} \times x^3 = \frac{2}{3}\sqrt{\pi} x^3$$ and finally $$\mathrm{Res}\left(Q(s)/x^s; s=-4\right) = \frac{1}{2} \times 1 \times \zeta(0) \times x^4 = - \frac{1}{4} x^4.$$

This gives the following expansion in a neighborhood of zero: $$S(x) \sim \frac{\pi^4}{90} - \frac{\pi^2}{6} x^2 + \frac{2}{3}\sqrt{\pi} x^3 - \frac{1}{4} x^4.$$

Since the sum being asked for is actually $S(\sqrt{t})$ we obtain $$S(\sqrt{t}) \sim \frac{\pi^4}{90} - \frac{\pi^2}{6} t + \frac{2}{3}\sqrt{\pi} t\sqrt{t} - \frac{1}{4} t^2.$$

This answer matches the results from the earlier posts, which deserve the credit, with this contribution being enrichment only.

Answer 3

As noted in other answers here, $f''(t)=\sum e^{-n^2t}$, which is the Riemann sum for $\int_0^{\infty}e^{-x^2t}dx=\sqrt{\pi/4t}$. So $f(t)$ will be the integral of the integral of that, or $(2/3)\sqrt{\pi}t^{3/2}$, plus At+B.