$$\arctan a+\arctan\left(\frac 1 a \right)=\frac \pi 2$$
I have the mark scheme in front of me, and I understand where the numbers come from, but I don't understand why they do what they do.
You need this part in to show it:
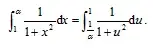
The markscheme says:

Again, I understand where the numbers come from, but can someone explain to me where the first line comes from, as well as the rest of it? It's a "Hence" question so I have to solve it this way.