Here is the problem I'm dealing with
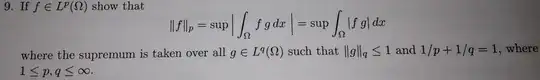
I'm not having success with...well, anything. Any hits on how I could get started and where I would go?
Here is the problem I'm dealing with
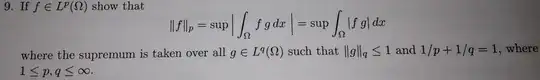
I'm not having success with...well, anything. Any hits on how I could get started and where I would go?
Three things to use: