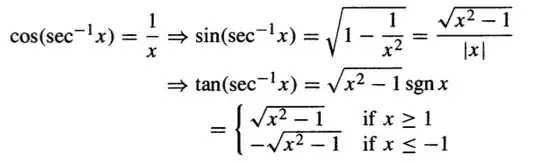$\tan \left(\sec ^{-1}(x)\right)$

Question

$$\tan \left(\sec ^{-1}(x)\right)$$

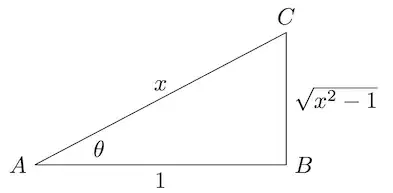
I know that sec(?)=$\frac{x}{1}$ and that sec=hyp/adj, therefore I conclude that hyp=x and adj=1 and that op=$\sqrt{x^2-1}$

Since Tan = opp/adj I thought the answer was the same as op. However I do not understand how this is done? cause my conclusion is wrong! The answer provided is this:

enter image description here

My conclusion is sqrt(x^2-1) however the answer is suppose to be sqrt(x^2-1)*sgn(x) — ALEXANDER, Sep 13 '14 at 19:44
Your conclusion is right when $x>0$. Only when $x<0$ is it incorrect. — Michael Hardy, Sep 13 '14 at 20:04

rae306 · Accepted Answer · 2014-09-14T11:36:23.740

5

enter image description here

In this triangle, we have:

$$\sec(\theta)=\frac{\text{hypotenuse}}{\text{adjacent}} \Rightarrow \theta=\sec^{-1}\Big(\frac{\text{hypotenuse}}{\text{adjacent}}\Big)$$

In your problem, $\theta=\sec^{-1}(x)$, so $\text{hypotenuse}=x$, $\text{adjacent}=1$ and $\text{opposite}=\sqrt{x^2-1}$ (Pythagorean Theorem).

Hence, $$\tan(\sec^{-1}x)=\tan(\theta)=\frac{\text{opposite}}{\text{adjacent}}=\dfrac{\sqrt{x^2-1}}{1}=\boxed{\sqrt{x^2-1}}$$

edited Sep 14 '14 at 11:36

answered Sep 13 '14 at 19:33

rae306

9,742

sqrt(x^2-1)*sgn(x) is suppose to be the answer – ALEXANDER Sep 13 '14 at 19:44
What is the source of this problem? – rae306 Sep 13 '14 at 19:56
Could you have a look at the updated question? I do not see what they have done – ALEXANDER Sep 14 '14 at 10:42
What is the name and the author of the book you're using? – rae306 Sep 14 '14 at 11:18

score 2 · Answer 2 · edited Sep 13 '14 at 19:21

2

Hint $$ \tan^2 u + 1 = \sec^2 u $$ and $$ \tan u = \pm\sqrt{\sec^2 u -1} $$ Can you see what happens when you place $u = \sec^{-1}x$?

edited Sep 13 '14 at 19:21

rae306

9,742

answered Sep 13 '14 at 19:14

Chinny84

14,186
2
22
31

$\tan \left(\sec ^{-1}(x)\right)$

2 Answers2