Proof - Area of a cyclic quadrilateral

Question

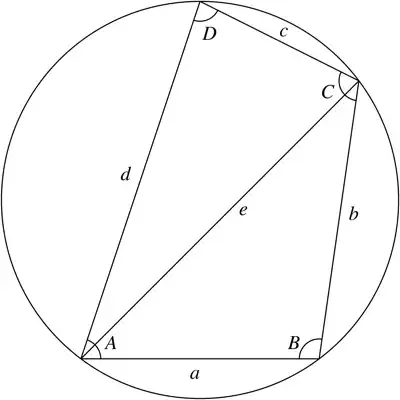
So we have a cyclic quadrilateral, as depicted below:

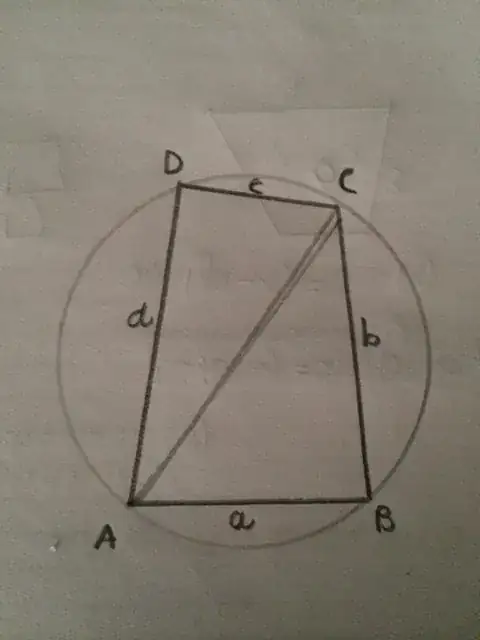
I have a conjecture that the area of this cyclic quadrilateral equals $$ \dfrac{\sqrt{(a+b+c-d)(a+b+d-c)(a+c+d-b)(b+c+d-a)}}{4} $$

I want to prove this. I know that the area of triangle ABC equals $\dfrac{1}{2}ab\sin(B)$ and the area of triangle ACD equals $\dfrac{1}{2}cd\sin(D)$. Seeing as $\sin(B) = \sin(D)$, I figured that the area of the quadrilateral equals $\dfrac{1}{2}(ab+cd)\sin(B)$.

But I'm stuck here. I have no clue how to get to the result I want. Can anyone provide an insight (and tell me whether or not my work up until now is valid)?

Answer 1

The Inscribed Angle Theorem shows that opposite angles of a cyclic quadrilateral are supplementary. Thus, $$ D=\pi-B $$ Therefore, $\cos(D)=-\cos(B)$ and $\sin(D)=\sin(B)$.

The Law of Cosines says $$ e^2=\overbrace{a^2+b^2-2ab\cos(B)}^{\text{as a side of $\triangle ABC$}}=\overbrace{c^2+d^2+2cd\cos(B)}^{\text{as a side of $\triangle ADC$}} $$ Solving for $\cos(B)$, we get $$ \cos(B)=\frac12\frac{a^2+b^2-c^2-d^2}{ab+cd} $$ Furthermore, $$ \begin{align} \frac14\sin^2(B) &=\frac{(2ab+2cd)^2-(a^2+b^2-c^2-d^2)^2}{16(ab+cd)^2}\\ &=\frac{\left((c+d)^2-(a-b)^2\right)\left((a+b)^2-(c-d)^2\right)}{16(ab+cd)^2}\\ &=\frac{((c+d+a-b)(c+d+b-a))((a+b+c-d)(a+b+d-c))}{16(ab+cd)^2}\\ &=\frac{(s-a)(s-b)(s-c)(s-d)}{(ab+cd)^2} \end{align} $$ where $s=\frac{a+b+c+d}2$ is the semi-perimeter.

The area of ${\large\unicode{x23E5}}ABCD\ \ $ is the sum of the area of $\triangle ABC=\frac12ab\sin(B)$ and the area of $\triangle ADC=\frac12cd\sin(D)$ $$ \frac12(ab+cd)\sin(B)=\sqrt{(s-a)(s-b)(s-c)(s-d)} $$ which, as Christian Blatter mentions, is called Brahmagupta's Formula.

Answer 2

These might be useful:

Heron's formula: $$\large \Delta=\sqrt{s(s-a)(s-b)(s-c)}$$

${}$

Ptolemy's theorem: $$\large AC.BD=ac+bd$$

Answer 3

This is Brahmagupta's formula; see here:

http://en.wikipedia.org/wiki/Brahmagupta%27s_formula