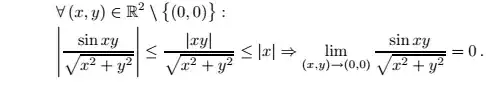2

Find the limit of the following function $f(x,y)$

$$\lim_{(x,y)\rightarrow (0,0)} \frac{\sin(xy)}{ \sqrt{x^2+y^2}}$$

What i did was to use polar coordinates,by letting $x=rcosa$ and $y=rsinb$ but because of

the $sin(xy)$ at the numerator, i dont think this method is suitable. I also tried

squeeze

theorem but since $sin(xy)$<$xy$ is not true when $xy$<0

i dont think this method works as

well. Could anyone help me with this. Thanks

ys wong
  • 2,017
  • Have you plotted the function? Do you think the limit exists? If so, what do you think the limit might be? – John Hughes Sep 10 '14 at 16:22
  • From the answer, i know that the limit is 0, but im unsure how to arrive there. – ys wong Sep 10 '14 at 16:25
  • $|\sin(xy)| \leq |xy|$ is always true. –  Sep 10 '14 at 16:26
  • 1
    Since you believe the answer is zero, you could try to show that the limit of the absolute value of your expression is zero (which would show, by the squeeze lemma, that the expression itself goes to zero). Once you decide to do that, @Bungo's hint will help. (Of course, you'll need to prove that his hint is correct as well!) – John Hughes Sep 10 '14 at 16:28
  • So i suppose i can use Bungo's assumption? Then that will be easy. – ys wong Sep 10 '14 at 16:32
  • I know how to use it but im unsure of the proof though. – ys wong Sep 10 '14 at 16:36
  • See the first answer here: http://math.stackexchange.com/questions/75130/how-to-prove-that-lim-limits-x-to0-frac-sin-xx-1 –  Sep 10 '14 at 16:45

3 Answers3

3

enter image description heremy solution ${}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}$

RE60K
  • 17,716
Joemak Boblinke
  • 119
  • 7
2

Note that $\forall (x,y)\ne (0,0)$ we have $$0\leq \left|\frac{\sin xy}{\sqrt{x^2+y^2}}\right|\leq \frac{|xy|}{\sqrt{x^2+y^2}}=\frac{|x|\cdot |y|}{\sqrt{x^2+y^2}}\leq \frac{\sqrt{x^2+y^2}\cdot |y|}{\sqrt{x^2+y^2}}=|y|, $$ i.e., $$0\leq \left|\frac{\sin xy}{\sqrt{x^2+y^2}}\right|\leq |y|, $$

and as $$\lim_{(x,y)\rightarrow (0,0)}0= 0 = \lim_{(x,y)\rightarrow (0,0)}|y|=0, $$ for the sandwisch theorem follow that $$\lim_{(x,y)\rightarrow (0,0)}\frac{\sin xy}{\sqrt{x^2+y^2}}=0. $$

ZHN
  • 1,419
1

Using polar coordinates $x=r\cos\theta$, $y=r\sin\theta$ we get:

$$\lim_{(x,y)\to(0,0)}\frac{\sin(xy)}{\sqrt{x^2+y^2}}=\lim_{\theta\to0}\frac{\sin(r\sin\theta r\cos\theta)}{\sqrt{r^2(\sin^2\theta+\cos^2\theta)}}=\frac0r=0$$

rae306
  • 9,742
  • Where's the $r$? I think you need to take $x = r \cos \theta$ and $y = r \sin \theta$. What you have just takes points on the unit circle. Also, as $\theta \to 0$, that just means you're approaching the $x$-axis, not the origin. I think you want $r \to 0$. – Viktor Vaughn Sep 10 '14 at 23:38