This happens due to insufficient precision to compute the values of F in that region. By default Mathematica uses machine precision, i.e. a fixed ~16 digits of decimal precision. This function F is likely prone to catastrophic cancellation.
The fix is to use Mathematica's arbitrary precision arithmetic, which also supports precision tracking. Since Mathematica has an estimate of the precision of the results, it can automatically increase the number of digits it uses internally to achieve a satisfactory result. It can also detect if the result has no significant digits. While it's not 100% reliable, this feature is very useful in practice.
To force the system to use its builtin arbitrary precision arithmetic, simply add the option WorkingPrecision -> 10 (or higher if necessary).
The computation from the screenshot is very slow, instead I recommend something like
PlotPoints -> 40, MaxRecursion -> 3, WorkingPrecision -> 10

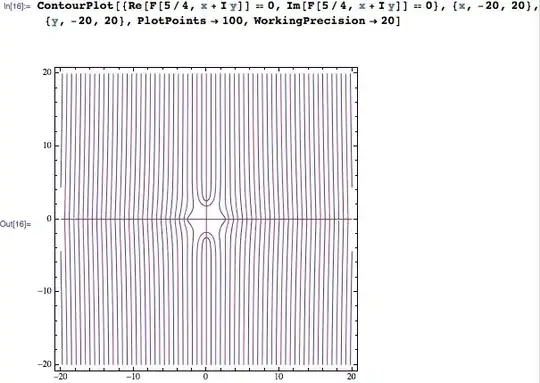
Fhas catastrophic cancellation. Anyway, setting aWorkingPrecisionfixes it, though it will be very slow. I usedWorkingPrecision -> 20andPlotPoints -> 100, though you can likely reduce that toWorkingPrecision -> 10andPlotPoints -> 50. It is not a high precision that you need here to fix it.WorkingPrecisiontriggers using Mma's built-in arbitrary precision arithmetic, which can do precision tracking. Thanks to precision tracking it knows ... – Szabolcs Sep 08 '14 at 21:29WorkingPrecision -> 10will likely work as well (haven't tried) even though it starts with fewer digits than the default machine precision. http://i.stack.imgur.com/ivOmy.png – Szabolcs Sep 08 '14 at 21:30