10

I believe the vector identity
$\vec{a} \times (\vec{b} \times \vec{c}) + \vec{b} \times (\vec{c} \times \vec{a}) + \vec{c} \times (\vec{a} \times \vec{b}) = 0$
is called the Jacobi identity and I know the proof.

Does anybody know of some elegant geometrical picture to illustrate why the identity is true?

Martin Sleziak
  • 53,687
Gerard
  • 1,513
  • Duplicate of http://math.stackexchange.com/questions/556009/geometric-interpretation-of-jacobi-identity-for-cross-product – almagest Sep 08 '14 at 20:12
  • 1
    perhaps, but it doesn't seem there is an adequate answer in the duplicate. – James S. Cook Sep 08 '14 at 20:13
  • Ýes a duplicate. I found an idea to use the property that the cross product gives a polarity on the real projective plane, when the vectors $\lambda \vec{a}$ etc. are considered as homogeneous coordinates. – Gerard Sep 08 '14 at 20:30
  • If three vectors add to zero, that means if you draw the vectors tip-to-tail then they'll form a triangle. That means they must all lie in one plane. So a geometrical proof would probably aim to construct a line perpendicular to this plane. – David H Sep 08 '14 at 20:33
  • In the link in the answer of the other question, the property of a triangle that its altitudes are concurrent is used and $A + B + C = 0$ gives the configuration of a triangle in a plane. – Gerard Sep 08 '14 at 20:33

3 Answers3

8

Here is an abstract nonsense proof:

The vector $$\vec T(\vec{a},\vec{b},\vec{c}):=\vec{a} \times (\vec{b} \times \vec{c}) + \vec{b} \times (\vec{c} \times \vec{a}) + \vec{c} \times (\vec{a} \times \vec{b})$$ is easily seen to be a skew trilinear function of the three vector variables $\vec{a}$, $\vec{b}$, $\vec{c}$. It follows that its coordinates $T_i$ are three real-valued such functions, whence are multiples of the determinant function (so-called triple vector product) $[\vec{a},\vec{b},\vec{c}]$ with factors $\lambda_i$ independent of $\vec{a}$, $\vec{b}$, $\vec{c}$. Putting $\vec{p}:=(\lambda_1,\lambda_2,\lambda_3)$ we therefore have $$\vec T(\vec{a},\vec{b},\vec{c})=[\vec{a},\vec{b},\vec{c}]\>\vec{p}$$ with a universal vector $\vec{p}$. This only makes sense when $\vec{p}=\vec{0}$.

Christian Blatter
  • 226,825
  • Why is it that the skew real-valued functions must be multiples of the triple vector product? – Gerard Dec 06 '14 at 21:50
  • 1
    It is a basic fact of multilinear algebra that in ${\mathbb R}^n$ there is, up to a constant factor, exactly one such skew $n$-linear function, also called volume form. – Christian Blatter Dec 07 '14 at 09:27
  • I followed the argument until the last sentence. Why is it true that this only makes sense when $p = 0$? My guess is that suitable choices of particular $a,b,c$ would yield a contradiction if $p\not = 0$, but I'm not sure which choices are the right ones. – Matthew Kvalheim Dec 09 '16 at 07:12
  • 1
    @MatthewKvalheim: Yes, use $$\vec{a} = \vec{i}, \vec{b} = \vec{j}, \vec{c} = \vec{k}$$. – Joshua P. Swanson Oct 26 '19 at 02:38
5

This attempt at an answer is geometric in the sense that it is stated in terms of vectors and not components.

Geometrically the double-cross product is given by $$\vec{a} \times (\vec{b} \times \vec{c}) = (\vec{a} \cdot \vec{c}) \vec{b}- (\vec{a} \cdot \vec{b}) \vec{c}.$$ This shows three things:

  1. $\vec{a} \times (\vec{b} \times \vec{c}) = (\vec{a} \cdot \vec{c}) \vec{b}- (\vec{a} \cdot \vec{b}) \vec{c}$ falls in the plane spanned by $\vec{b}$ and $\vec{c}$
  2. $\vec{b} \times (\vec{c} \times \vec{a}) = (\vec{b} \cdot \vec{a}) \vec{c}- (\vec{b} \cdot \vec{c}) \vec{a}$ falls in the plane spanned by $\vec{c}$ and $\vec{a}$
  3. $\vec{c} \times (\vec{a} \times \vec{b}) = (\vec{c} \cdot \vec{b}) \vec{a} - (\vec{c} \cdot \vec{a}) \vec{b}$ falls in the plane spanned by $\vec{a}$ and $\vec{b}$

Add these relations the terms in the $\vec{a},\vec{b}$ and $\vec{c}$ directions cancel thus revealing the Jacobi Identity.

We could visualize these in terms of three planes which intersect along the directions $\vec{a},\vec{b}, \vec{c}$. I illustrate as if they are orthogonal as to keep the picture manageable. The idea here is the lengths of the orange, purple and cyan arrows are indicative of the dot-products which appear in the spans.

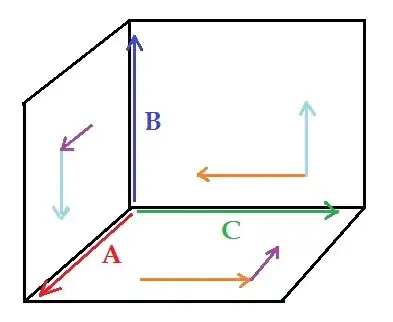
enter image description here

James S. Cook
  • 16,755
  • The basic geometric idea here is also used in this http://math.stackexchange.com/a/400732/36530 – James S. Cook Sep 15 '14 at 02:20
  • This answer is fine in terms of explaining the direction of the vector triple product. But could you explain why the magnitude of each component is the way it is? i.e = the dot product of two other vectors. – A Slow Learner Apr 16 '18 at 05:29
1

Answering to Matthew Kvalheim. Let $R:\mathbb{R}^3\rightarrow \mathbb{R}^3$ be a rotation on $\mathbb{R}^3$ around a certain axis. Then $(R\vec{a}\times R\vec{b})=R(\vec{a}\times\vec{b})$. From here and the definition of the map $\vec{T}$ we have that $$ \vec{T}(R\vec{a},R\vec{b},R\vec{c})=R\vec{T}(\vec{a},\vec{b},\vec{c}). $$ From the expression in terms of $\vec{p}$ of the map $\vec{T}$ and the fact that $[R\vec{a},R\vec{b},R\vec{c}]=[\vec{a},\vec{b},\vec{c}]$, one obtains $$ \vec{T}(R\vec{a},R\vec{b},R\vec{c})=[R\vec{a},R\vec{b},R\vec{c}]\vec{p}=[\vec{a},\vec{b},\vec{c}]\vec{p}=\vec{T}(\vec{a},\vec{b},\vec{c}). $$ Comparing the above expressions, we obtain that
$$ R\vec{T}(\vec{a},\vec{b},\vec{c})=\vec{T}(\vec{a},\vec{b},\vec{c}) $$ for every $R$, which means that $\vec{T}(\vec{a},\vec{b},\vec{c})=0$ for arbitrary $\vec{a},\vec{b},\vec{c}$ and $\vec{p}=0$ always.

Javier
  • 121