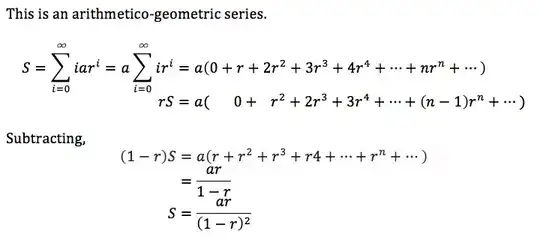increasing geometric series

Question

I need to find the summation of:

$$\begin{align*} &\sum_{i=0}^{\infty} iar^{i} &\text{if }|r|\lt 1 \end{align*}$$

I found this result: $$\begin{align*} \frac{a}{1-r} &= \sum_{i=0}^{\infty}ar^i &\text{if }|r|\lt 1\\ \frac{d}{dr}\frac{a}{1-r} &=\frac{d}{dr}\sum_{i=0}^{\infty}ar^i&\text{if }|r|\lt 1\\ \frac{a}{(1-r)^2} &= \sum_{i=0}^{\infty}\frac{d}{dr}ar^i &\text{if }|r|\lt 1\\ \frac{a}{(1-r)^2} &= \sum_{i=0}^{\infty} iar^{i-1}&\text{if }|r|\lt 1\\ \frac{a}{(1-r)^2} &=\sum_{i=1}^{\infty} iar^{i-1} &\text{if }|r|\lt 1 \end{align*}$$

However I do not get the last step. Shouldn't it be:

$$\begin{align*} \frac{a}{(1-r)^2} &= \sum_{i=0}^{\infty} iar^{i-1}&\text{if }|r|\lt 1\\ \frac{ar}{(1-r)^2} &=\sum_{i=0}^{\infty} iar^{i} &\text{if }|r|\lt 1 \end{align*}$$

Thank you

Answer 1

When $i=0$, the term is zero, as it's multiplied by $i$, hence the summation from $i=0$ is the same as summation from $i=1$.

Here's an alternative derivation.

Answer 2

$$\frac{a}{(1-r)^2}=\sum_{i=1}^\infty iar^{i-1}\iff \frac{a}{(1-r)^2}=\frac{1}{r}\sum_{i=1}^\infty iar^i$$ I guess for some reason this step was omitted but both answers are correct except the first one doesn't answer the question.