Monotone functions are continuous except countably many points. If function is Riemann integrable it has only a finite number of discontinuity points. So how monotone functions are Riemann integrable on closed interval always?
Asked
Active
Viewed 4,762 times
0
-
3"If function is Riemann integrable it has only a finite number of discontinuity points." That's not true; consider the function $f(x)=\begin{cases}1/2&\text{if $1/2<x\le1$,}\1/4&\text{if $1/4<x\le1/2$,}\1/8&\text{if $1/8<x\le1/4$,}\&\vdots\0&\text{if $0=x$}\end{cases}$ on the interval $[0,1]$. – Sep 05 '14 at 20:31
-
2Using the measure of the set of discontinuities is fairly high tech. One can prove that monotone functions are Riemann integrable using the definition. – Ayman Hourieh Sep 05 '14 at 20:35
1 Answers
14
Suppose $f$ is nondecreasing. For any partition $a = x_0 < x_1 \ldots < x_n = b$ of your interval $[a,b]$, any Riemann sum is between the left Riemann sum $L = \sum_{j=1}^n f(x_{j-1})(x_j - x_{j-1})$ and the right Riemann sum $R = \sum_{j=1}^n f(x_{j})(x_j - x_{j-1})$. The difference between them is at most $(f(b) - f(a)) \delta$ where $\delta = \max_j (x_j - x_{j-1})$.
Proof without words:
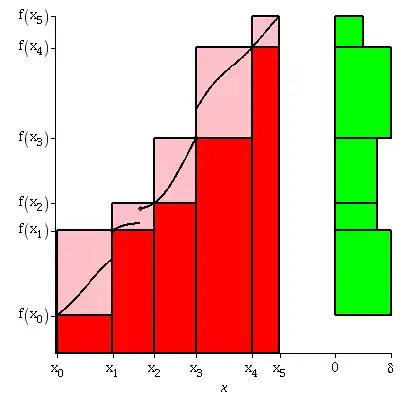
Robert Israel
- 448,999
-
Seems like one should do the proof without words using a discontinuous function, otherwise the most general phenomena is not observed. – RghtHndSd Sep 05 '14 at 21:09
-
-
-
By the way, the argument (and the picture) go back to Newton who, of course, did not note that this was really the theorem he was establishing. – Andrés E. Caicedo Sep 05 '14 at 21:36
-