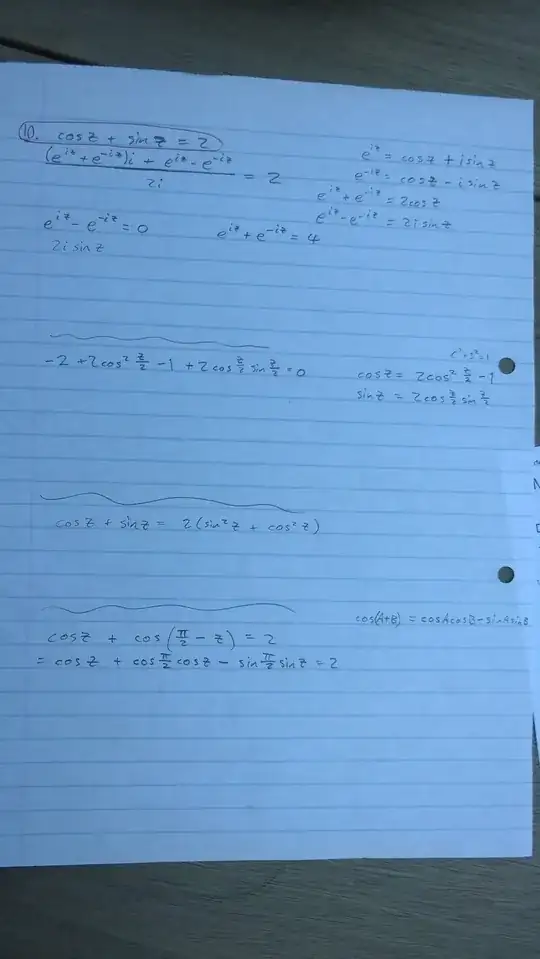Solve $\cos{z}+\sin{z}=2$

Question

I am trying to solve the question:

$\cos{z}+\sin{z}=2$

<p>Where $z \in \mathbb{C}$</p>

I think I know how to solve $\cos{z}+\sin{z}=-1$:

$1+2\cos^2{\frac{z}{2}}-1+2\sin \frac{z}{2}\cos{\frac{z}{2}}=0\\ 2\cos{\frac{z}{2}}(\cos{\frac{z}{2}}+\sin{\frac{z}{2}})=0$

etc... (that is, if the double angle identity holds true when the 'angle' is a complex number - I might be wrong about this)

My other methods involve:

• trying to substitute $\cos{z}=\frac{e^{iz}+e^{-iz}}{2}$ and $\sin{z}=\frac{e^{iz}-e^{-iz}}{2i}$. This seems to be the most obvious method, but I can't work out the next step after $$e^{iz}-e^{-iz}+(e^{iz}+e^{-iz})i=4i$$

• substituting $2=2(\sin^2{z}+\cos^2{z})$

• substituting $\sin{z}=\cos(\frac{\pi}{2}-z)$ (again, not really sure if this can be done)

Answer 1

Recall that the addition formula for cosines reads $$\cos(z+z')=\cos z\cos z'-\sin z\sin z',$$ and that, for $z'=-\pi/4$, one gets $$\cos(z-\pi/4)=(\cos z+\sin z)/\sqrt2.$$ Hence the equation to be solved is $$\cos(z-\pi/4)=\sqrt2.$$ To go further, consider $$u=\mathrm e^{\mathrm i(z-\pi/4)},$$ then $u\ne0$ and the equation above reads $$u+u^{-1}=2\sqrt2,$$ that is, $$u^2-2\sqrt2u+1=0=(u-\sqrt2)^2-1,$$ that is, $$u=\sqrt2\pm1.$$ Thus, the complex number $$\mathrm i(z-\pi/4)-\log(\sqrt2\pm1)$$ must be a multiple of $2\mathrm i\pi$, that is, finally, and since $\sqrt2\pm1$ are respective inverses, $$z=\pm\mathrm i\log(\sqrt2+1)+\pi/4+2n\pi,\qquad n\in\mathbb Z.$$ Note that here, $\log$ is the usual function logarithm defined on the positive real half-line.

Answer 2

A hint: The formula $$\cos x+\sin x=\sqrt{2}\>\sin\left(x+{\pi\over4}\right)$$ known from high-school trigonometry also holds for complex $x$.

Answer 3

Yet another answer:

First, let's recognize why we need to go to complex variables. Recalling that $\cos\frac{\pi}{4}=\sin\frac{\pi}{4}=\frac{1}{\sqrt{2}}$, we have from the cosine addition formula

$$\sin z+\cos z = \sqrt{2}\cdot\left[\sin\frac{\pi}{4}\sin z+\cos\frac{\pi}{4}\cos z\right]=\sqrt{2}\cos\left(z-\frac{\pi}{4}\right)$$ as several other answers have already noted. This has a maximum value of $\sqrt{2}$ for real $z$, so we'll need complex $z$ if we want to get a value of $2$ instead.

Keeping in mind that the closest approach for real $z$ was $z=\pi/4$, we make the substitution $z=\frac{\pi}{4}+i\tau$ with the anticipation that $\tau$ should 'mostly' be imaginary. Thus gives the equation $$\sqrt{2}\cos\left(z-\frac{\pi}{4}\right)=\sqrt{2}\cos(i\tau)=\sqrt{2}\cosh \tau=2$$ which immediately yields $\tau=\pm \cosh^{-1} \sqrt{2}$ as the principal solutions (recall that hyperbolic cosine is an even function). Thus $\boxed{z=\dfrac{\pi}{4}\pm i\cosh^{-1} \sqrt{2}+2\pi n}$ where we have taken into account the $2\pi$-periodicity of the trig functions involved.

Answer 4

Note that

$$\cos(\arctan(z)) + \sin(\arctan(z)) = \frac{1}{\sqrt{1+z^2}} + \frac{z}{\sqrt{1+z^2}}.$$

So, if you can solve the equation

$$\frac{1}{\sqrt{1+z^2}} + \frac{z}{\sqrt{1+z^2}} = 2,$$

(which is quadratic) then you can solve the original.

Answer 5

I think you were on the right track. Putting $\;z=x+iy\;,\;\;x,y\in\Bbb R\;$ :

$$e^{iz}-e^{-iz}+(e^{iz}+e^{-iz})i=4i\implies e^{-y+ix}-e^{y-ix}+\left(e^{-y+ix}+e^{y-ix}\right)i=4i\iff$$

$$e^y\left(\cos x-i\sin x+i(\cos x-i\sin x)\right)+e^{-y}\left(\cos x+i\sin x+i(\cos x+i\sin x)\right)=4i\iff$$

$$e^y\left(\cos x+\sin x\right)+e^{-y}\left(\cos x-\sin x\right)+\left[e^y\left(\cos x-\sin x\right)+e^{-y}\left(\cos x+\sin x\right)\right]i=4i$$

And thus you get two equations:

$$\begin{align*}e^y\left(\cos x+\sin x\right)+e^{-y}\left(\cos x-\sin x\right)=0\\e^y\left(\cos x-\sin x\right)+e^{-y}\left(\cos x+\sin x\right)=4\end{align*}$$

If you add\substract both equations you get

$$\cos x\left(e^y+e^{-y}\right)=2\iff\cos x\cosh x=1$$

$$\sin x\left(e^y-e^{-y}\right)=-2\iff \sin x\sinh x=-1$$

You now have two transcendental, real equations to solve

Answer 6

Now here is a purely algebraic solution. As you have noted, the problem is equivalent to $$(1 + i){e^{iz}} - (1 - i){e^{ - iz}} = 4i$$consider the new variable $x$ as ${x=e^{iz}}$in terms of the newly defined variable, the problem reads as$$(1 + i)x - {{(1 - i)} \over x} = 4i$$multiplying by $x$, we get $$(1 + i){x^2} - 4ix - (1 - i) = 0$$which is a standard second order equation. The solutions are $$x = {{4i \pm \sqrt { - 16 + 4(1 - i)(1 + i)} } \over {2(1 + i)}} = \left( {1 \pm {{\sqrt 2 } \over 2}} \right)(1 + i)$$so that $$z = {1 \over i}\ln x = - i\left( {\ln \left( {1 \pm {{\sqrt 2 } \over 2}} \right) + \ln (1 + i)} \right)$$which is hopefully what you are looking for (note that a more careful analysis in the logarithm part yields solutions in higher Riemann planes).