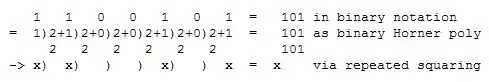Consider some function $f : \{1,2,\ldots,n\} \rightarrow \{1,2,\ldots,n\}$. I want to calculate $f^x$. It can be easily done in time $O(nx)$ where $n$ is the number of elements in the set.
I've found some formula $f^{2k+1} = f^{2k} f $ and my source says we can use this to do fast binary exponentiation. In fact I know how to calculate $a^x$ where $a$ is some integer using fast binary exponentiation, but I have no idea how to do it for functions/permutations.
Thanks for any hints.
Note that function application is associative, so $f^{2k+1}=f^{2k}\cdot f=(f^k)^2 *f(k)$. Where $^2$ means double application. The usual applications of fast binary exponentiation are either real numbers or matrices. Matrices can represent linear functions, and permutations are linear maps, so with naive matrix multiplication, you would obtain a $O(n^3 \log x)$ algorithm, which would only be faster for significantly large values of $x$.
But permutations are even more special. You have the cycle decomposition, which can be computed in linear ($O(n)$) time. Once you have the cycle representation, it is easy to compute iterated application. For general functions, the cycles might start with a chain, but the method would still work.
Repeated squaring may be used to compute powers of any associative binary operation, i.e. it works in any semigroup. In particular, since function composition $\rm\:f\circ g\:$ is associative, it may be use to compute compositional powers of functions $\rm\:f^2 =\: f\circ f\:,\:$ etc. However, one should beware that repeated squaring can be much less efficient than repeated multiplication in contexts where the cost of multiplication and squaring depends on the size of the operands; for example, look up work by Richard Fateman on computing powers of sparse polynomials.
Note that the algorithm is easily memorized or reconstructed since it arises simply from writing the exponent in binary radix in Horner polynomial form, i.e. $\rm\ d_0 + x\ (d_1 + x\ (d_2\ +\:\cdots))\:$ for $\rm\:x=2\:.\:$ Below is an example of computing $\rm\ x^{101}\ $ by repeated squaring. Note that the repeated square form arises simply from performing various substitutions into the binary polynomial Horner form namely $\rm\ 1\to x,\ \ 0\to 1,\ \ (x)\:2\to (x)^2\ $ into $101_{10} = 1100101_2\ $ expanded into Horner form, viz.
A nice way to think about it is to notice that a function from any finite set to itself can be represented as a tuple, with the $i$th element giving the image of $i$ under the function: for example, $(2,3,4,1)$ is a representation of a function from the set $\{1,2,3,4\}$ to itself.
I'll write all my code using MATLAB syntax, as I think it's particularly easy to read, and arrays index from 1, which is sometimes pleasant for mathematicians.
Function composition is composition of tuples, and it can be computed in linear time:
function h = compose(f,g)
disp('Called compose')
for i = 1:length(f)
h(i) = f(g(i));
end
end
I've inserted a line to display a message every time the function composition routine is called. The squaring operator is then easily defined:
function f2 = square(f)
f2 = compose(f,f);
end
And finally our exponentiation routine is:
function h = exponentiate(f,n)
if n == 1 % The base case
h = f;
elseif mod(n,2) == 0
g = exponentiate(f,n/2);
h = square(g);
else
g = exponentiate(f,(n-1)/2);
h = compose(f,square(g));
end
end
We can now define a function and exponentiate it:
>> f = [2,3,4,5,1];
>> exponentiate(f,2)
Called compose
ans =
3 4 5 1 2
>> exponentiate(f,16)
Called compose
Called compose
Called compose
Called compose
ans =
2 3 4 5 1
>> exponentiate(f,63)
Called compose
Called compose
Called compose
Called compose
Called compose
Called compose
Called compose
Called compose
Called compose
Called compose
ans =
4 5 1 2 3
And there you have it - the composition function is called approximately $\log_2(x)$ times when we compose the function with itself $x$ times. It takes $O(n)$ time to do the function composition and $O(\log x)$ calls to the composition routine, for a total time complexity of $O(n\log x)$.
