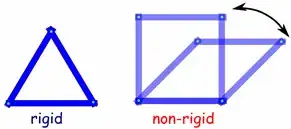
How do you find the area of a convex quadrilateral $ABCD$, given only the length of its sides $a$, $b$, $c$ and $d$. If the length of a single diagonal is given, I could easily find its area by dividing it into two triangles and applying Heron's formula to each.
I encountered this problem while trying to find the area of a patch of land. Sometimes, the area maybe approximated by a rectangle or a trapezium or some other simple figure, but in general opposite sides are not parallel. All the formulas I have so far seen includes knowing at least one angle or a diagonal.
So is there a formula (even a complicated one maybe) that gives the area of a quadrilateral given only its side lengths?