proof that union of a sequence of countable sets is countable.

Question

This is a theorem proved in Rudin.

Theorem. Let $E_n, n=1,2,3,\ldots$ be a sequence of countable sets, and put $S=\bigcup_{n=1}^\infty E_n$. Then $S$ is countable.

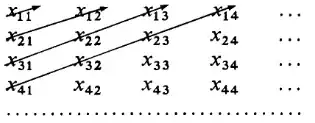
Proof. Let every set $E_n$ be arranged in a sequence $x_{nk}, k=1,2,3,\ldots$, and consider the infinite array $$\begin{array}{cccc} x_{11}&x_{12}&x_{13}&\cdots\\ x_{21}&x_{22}&x_{23}&\cdots\\ x_{31}&x_{32}&x_{33}&\cdots\\ \vdots&\vdots&\vdots&\ddots \end{array}$$ in which elements of $E_n$ form the $n$th row. The array contains all elements of $S$. As indicated by the arrows in this picture —

— these elements can be arranged in a sequence $$x_{11};x_{21},x_{12};x_{31},x_{22},x_{13};x_{41},x_{32},x_{23},x_{14};\ldots.\qquad(17)$$ If any two of the sets $E_n$ have elements in common, these will appear more than once in $(17)$. Hence there is a subset $T$ of the set of all positive integers such that $S\sim T$, which shows that $S$ is at most countable (Theorem 2.8). Since $E_1\subset S$ and $E_1$ is infinite, $S$ is infinite, and thus countable.

I've a hard time visualizing/understanding the last part of the proof though[(17) onwards], will someone please give an intuitive explanation/description of the last paragraph to help me in understanding the proof?

Answer 1

The idea in the last paragraph is that in this sequence we many name the same element twice. This can happen if some $x$ is in two of the $E_k$ sets. Hence the author points out that the function that sends every natural number $n$ to the $n$th element of that sequence is not bijective. To make it bijective, we have to restrict its domain to some subset of the natural numbers (such that not two natural numbers are sent to the same element). Hence, $S$ is equinumerous with a subset of natural numbers.

Now we know (and I assume this is theorem 2.8) that every subset of the natural numbers is either countably infinite or finite. Therefore up until now we have only shown that $S$ is either countably infinite or finite. But, we already know that it contains at least countably infinite elements, the elements of $E_1$. Hence it cannot be finite. This implies that it is countable.

Answer 2

What Rudin is saying is that in the sequence which he writes down, every element of every $E_n$ appears at least once. By definition, this shows that there exists a surjection $\mathbb{N} \to S$. Hence $S$ can be identified with a subset of the positive integers: for each $s \in S$, $s$ appears at some point in the sequence and we can let $m(s)$ denote any one of those integers such that the $m(s)$-th element in the sequence is $s$. Hence $S$ is either finite or countably infinite. The first case is excluded since $S$ contains the infinite set $E_1$.