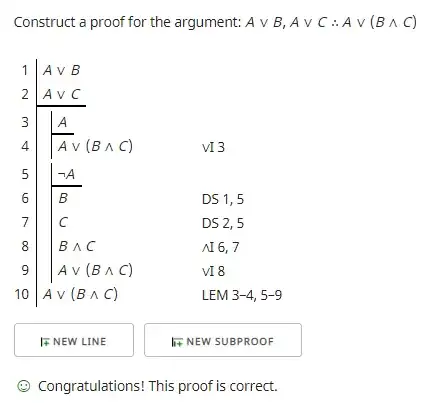
I am desperately trying to figure out the formal proof for this argument.
$$\begin{array}{r} A\lor B\\ A\lor C\\ \hline A\lor (B \land C) \end{array}$$
I am trying to apply the backwards method here. I am trying to infer A, in order to use vIntro in the last step and introduce the final disjunction. But I got stuck finding sufficient proof for A.
Any hint will be greatly appreciated. Thank you!