How to prove $\int^{\pi/2}_0 \log{\cos{x}} \, \mathrm{d}x = \frac{\pi}{2}\log\left(\frac12\right)$

Question

ALREADY ANSWERED

I was trying to prove the result that the OP of this question is given as a hint.

That is to say: imagine that you are not given the hint and you need to evaluate:

$$I = \int^{\pi/2}_0 \log{\cos{x}} \, \mathrm{d}x \color{red}{\overset{?}{=} }\frac{\pi}{2} \log{\frac{1}{2}} \tag{1}$$

How would you proceed?

---

Well, I tried the following steps and, despite it seems that I am almost there, I have found some troubles:

• Taking advantage of the fact: $$\cos{x} = \frac{e^{ix}+e^{-ix}}{2}, \quad \forall x \in \mathbb{R}$$
• Plugging this into the integral and performing the change of variable $z = e^{ix}$, so the line integral becomes a contour integral over a quarter of circumference of unity radius centered at $z=0$, i.e.: $$ I = \frac{1}{4i} \oint_{|z|=1}\left[ \log{ \left(z+\frac{1}{z}\right)} - \log{2} \right] \, \frac{\mathrm{d}z }{z}$$

$\color{red}{\text{We cannot do this because the integrand is not holomorphic on } |z| = 1 }$

• Note that the integrand has only one pole lying in the region enclosed by the curve $\gamma : |z|=1$ and it is holomorphic (is it?) almost everywhere (except in $z =0$), so the residue theorem tells us that:

$$I = \frac{1}{4i} \times 2\pi i \times \lim_{z\to0} \color{red}{z} \frac{1}{\color{red}{z}} \left[ \underbrace{ \log{ \left(z+\frac{1}{z}\right)} }_{L} - \log{2} \right] $$

• As I said before, it seems that I am almost there, since the result given by eq. (1) follows iff $L = 0$, which is not true (I have tried L'Hôpital and some algebraic manipulations).

Where did my reasoning fail? Any helping hand?

Thank you in advance, cheers!

---

Please note that I'm not much of an expert in either complex analysis or complex integration so please forgive me if this is trivial.

---

Notation: $\log{x}$ means $\ln{x}$.

---

A graph of the function $f(z) = \log{(z+1/z)}$ helps to understand the difficulties:

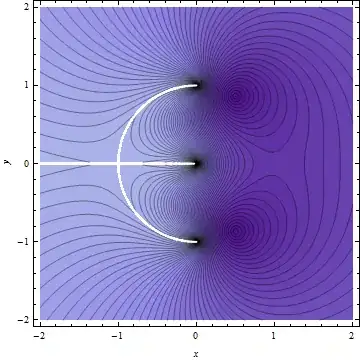
where $|f(z)|$, $z = x+i y$ is plotted and the white path shows where $f$ is not holomorphic.

Answer 1

An other way:

Firstly $$\int_0^{\pi/2}\ln(\cos t)dt\underset{t=\frac{\pi}{2}-u}{=}\int_{0}^{\pi/2}\ln\left(\cos\left(\frac{\pi}{2}-u\right)\right)du=\int_0^{\pi/2}\ln(\sin u)du \tag 1 $$

Then, $$\int_0^{\pi/2}\ln(\sin t)dt=\frac{1}{2}\left(\int_{0}^{\pi/2}\ln(\sin t)dt+\int_0^{\pi/2}\ln(\cos t)dt\right)=\frac{1}{2}\int_0^{\pi/2}\ln\left(\frac{\sin(2t)}{2}\right)dt\underset{r=2t}{=}\frac{1}{4}\int_0^\pi\ln\left(\frac{\sin r}{2}\right)dr=\frac{1}{4}\int_{0}^\pi\ln(\sin r)dr-\frac{\pi\ln 2}{4}\underset{Chasles}{=}\frac{1}{4}\int_0^{\pi/2}\ln(\sin r)dr+\int_{\pi/2}^\pi\ln(\sin t)dt-\frac{\pi\ln 2}{4}\underset{t=r+\frac{\pi}{2}}{=}\frac{1}{4}\int_0^{\pi/2}\ln(\sin r)dr+\frac{1}{4}\int_0^{\pi/2}\ln(\sin t)dt=\frac{1}{2}\int_0^{\pi/2}\ln(\sin t)dt-\frac{\pi\ln 2}{2}$$

And thus $$\int_0^{\pi/2}\ln(\sin t)dt=\frac{1}{2}\int_0^{\pi/2}\ln(\sin t)dt-\frac{\pi\ln 2}{4}\iff\int_0^{\pi/2}\ln(\sin t)dt=-\frac{\pi\ln 2}{2}.$$

By $(1)$ we conclude that $$\int_0^{\pi/2}\ln(\cos t)dt=-\frac{\pi\ln 2}{2}$$

Answer 2

As shown by @idm, we have that $$ \int_0^{\pi/2}\ln(\cos(x))dx = \int_0^{\pi/2}\ln(\sin(x))dx. $$ We can exploit this identity for another one and use Feynman's method (differentiating under the integral). Consider $$ \int_0^{\pi/2}x\cot(x)dx.\tag{1} $$ By integration by parts, we have $$ \int_0^{\pi/2}x\cot(x)dx = x\ln(\sin(x))\Bigr|_0^{\pi/2} - \int_0^{\pi/2}\ln(\sin(x))dx = - \int_0^{\pi/2}\ln(\sin(x))dx $$ since $\lim_{x\to 0}x\ln(\sin(x)) = 0$. Therefore, we can evaluate the negative of equation $(1)$. \begin{align} I(\alpha) &= \int_0^{\pi/2}\arctan(\alpha\tan(x))\cot(x)dx\tag{2}\\ I'(\alpha) &= \int_0^{\pi/2}\frac{\partial}{\partial\alpha}\Bigl[\arctan(\alpha\tan(x))\cot(x)\Bigr]dx\\ &= \int_0^{\pi/2}\frac{dx}{\alpha^2\tan^2(x) + 1}\\ &= \frac{\pi}{2(\alpha +1)}\\ I(\alpha) &= \frac{\pi}{2}\ln(\alpha + 1) + C \end{align} Thus, $I(0)\Rightarrow C=0$ so $$ I(\alpha) = \frac{\pi}{2}\ln(\alpha + 1) $$ We recover equation $(1)$ from equation $(2)$ when $\alpha = 1$ so $I(1) = \frac{\pi}{2}\ln(2)$ and since $$ \int_0^{\pi/2}\ln(\sin(x))dx = -\int_0^{\pi/2}x\cot(x)dx = -\frac{\pi}{2}\ln(2), $$ we have $$ \int_0^{\pi/2}\ln(\sin(x))dx = -\frac{\pi}{2}\ln(2), $$

Answer 3

Since this post was tagged with complex analysis, I can provide a contour integration solution as well. Again, I will exploit the identity given to you by @idm. $$ \int_0^{\pi/2}\ln(\sin(\theta))d\theta = \frac{1}{2}\int_0^{\pi}\ln(\sin(\theta))d\theta $$ Consider $1 - e^{2iz} = -2ie^{iz}\sin(z)$. We can write $1 - e^{2iz}$ as $$ 1 - e^{-2y}(\cos(2x) + i\sin(2x)) < 0\text{ when } x=\pi n, \ y\leq 0 $$ Now let's consider the contour from $0$ to $\pi$ to $\pi + iA$ to $iA$ where we take a quarter of a circle around $0$ and $\pi$ with radius $\epsilon$. From the periodicity of the function, the vertical line segments cancel each other since they have opposite signs. Additionally, as $A\to\infty$, the top integral of the top line goes to zero and as $\epsilon\to 0$, the integral around $0$ and $\pi$ go to zero. \begin{align} \ln(-2ie^{ix}\sin(z)) &= \ln(-2i) + \ln(e^{ix}) + \ln(\sin(\theta))\\ &= \ln|-2i| + i\arg(-2i) + ix + \ln(\sin(\theta))\\ &= \ln(2) - i\frac{\pi}{2} + \ln(\sin(\theta)) + i\frac{\pi}{2} \end{align} where $\ln(2i) = \ln(2) + i\arg(-2i)$ and we take the principle argument to be $-\frac{\pi}{2}$ and the imaginary part of $ix$ is between $0$ and $\pi$. Since there are no poles in them contour, by the Cauchy integral formula, the integral is equal to zero. \begin{alignat}{2} \int_0^{\pi/2}\ln(\sin(\theta))d\theta &=\frac{1}{2}\int_0^{\pi}\ln(\sin(\theta))d\theta\\ &= \frac{\ln(2)}{2}\int_0^{\pi}d\theta - \frac{i\pi}{4}\int_0^{\pi}d\theta + \frac{1}{2}\int_0^{\pi}\ln(\sin(\theta))d\theta + \frac{i\pi}{4}\int_0^{\pi}d\theta &&{}= 0\\ &= \frac{\pi\ln(2)}{2} - \frac{i\pi^2}{4} + \frac{1}{2}\int_0^{\pi}\ln(\sin(\theta))d\theta + \frac{i\pi^2}{4} &&{}=0\\ \frac{1}{2}\int_0^{\pi}\ln(\sin(\theta))d\theta &= -\frac{\pi\ln(2)}{2}\\ \int_0^{\pi/2}\ln(\sin(\theta))d\theta &= -\frac{\pi\ln(2)}{2} \end{alignat}

Answer 4

Hint: with $\cos x=u$ $$\int_0^{\pi/2}\log\cos x\mathrm{d}x=-\int_0^1\frac{\log u}{\sqrt{1-u^2}}\mathrm{d}u$$