rationalize the complex number multiplication rule

Question

For a middle school student without previous knowledge of complex number, how do one introduce the multiplication rules of complex number? i.e., if we have two real number pairs of $(a,b)$ and $(c,d)$, why do we define a product of $(a,b) * (c,d) = (ac-bd, ad+bc)$? I wanted to start here and introduce the $i$ and polar expression of complex number as a consequence.

Answer 1

You could explain it in terms of rotation.

Suppose you have a point $(a,b)$ in the plane. If you multiply it by a real number $s$ then you scale the length but preserve the direction, $(sa,sb)$. What if we want to multiply two vectors together in a way that multiplies their lengths together and adds their polar angles?

This would allow us to rotate points just by multiplying them... etc

---

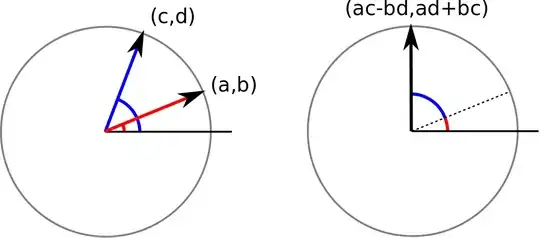
Personally I feel that introducing $i$ and building from there is a more natural approach though.

Answer 2

I hope it's never too late for an answer.

Approach 1.

This approach uses similar triangle to define multiplication and Thales's theorem (intercept theorem) to rationalize it.

The multiplication of complex numbers can be introduced first geometrically via the complex plane. The geometrical construction involves certain analogies between real numbers and the real line so it best to start with a visualization of multiplication of real numbers on the real line.

Geometric construction

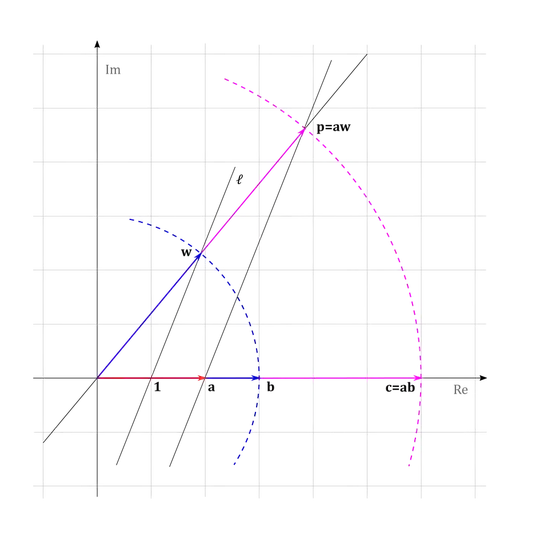
We start with a visualization of multiplication of real numbers using Thales's theorem.

Draw a real line with an fixed origin $\mathbf{0}$ and a point $\mathbf{1}$ that defines a unit of length. Now real numbers $a, b\in \mathbb{R}$ correspond to unique points on the real line that are $a$ (respectively $b$) times the unit of length $\mathbf{a}=a\mathbf{1}$, $\mathbf{b}= b\mathbf{1}$.

Draw a line through the origin and find a point $\mathbf{w}$ that is $b$ away from the origin. Draw a line $\ell$ through $\mathbf{1}$ and $\mathbf{w}$. Draw a parallel line to $\ell$ through $\mathbf{b}$ and find the point $\mathbf{p}$ where lines intersect. Transfer the point $\mathbf{p}$ to the real line to get a point $\mathbf{c}$. Let's denote the distance of $\mathbf{p}$ and $\mathbf{c}$ from the origin by $p$. From the Thales's theorem we get

$$ \frac{p}{a} = \frac{b}{1}, $$

so $p=a\cdot b$, so the point $\mathbf{c}$ is the same as $(a\cdot b)\mathbf{1}$.

The construction justifies as well defining $\mathbf{p}$ as a product of $a\mathbf{w}$ for any $\mathbf{w}$ not on the real line. So $\mathbf{a\cdot w}$ is defined for any point $\mathbf{a}$ on the real line and any point $\mathbf{w}$.

We notice that the triangles $\mathbf{0, 1, w}$ and $\mathbf{0, a, a\cdot w}$ are similar. We take this as a defining property of multiplication for any points $\mathbf{z}$ and $\mathbf{w}$.

Definition. The product of $\mathbf{z}$ and $\mathbf{w}$ is a unique point $\mathbf{z} \cdot \mathbf{w}$ such the triangles $\mathbf{0, 1, w}$ and $\mathbf{0, z, z\cdot w}$ are similar.

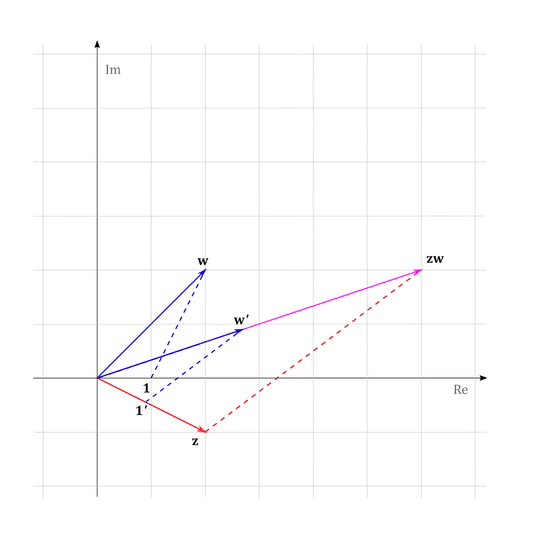
In general case, the product $\mathbf{z \cdot w}$ be constructed as follows:

Draw a circle centred at $\mathbf{0}$ of radius 1 and find the intersection point $\mathbf{1'}$ with a line through $\mathbf{0}$ and $\mathbf{z}$. Draw a circus centred at $\mathbf{0}$ of radius $|\mathbf{0w}|$ and another one centred at $\mathbf{1'}$ of radius $|\mathbf{1w}|$. Find the intersection point $\mathbf{w'}$. The constructed triangle $\mathbf{0, 1', w'}$ should be oriented the same as the original triangle, it should not be reflected. Draw a line through $\mathbf{0}$ and $\mathbf{w'}$ another one through $\mathbf{1'}$ and $\mathbf{w'}$. From this moment on, we follow the construction for real numbers. Draw a parallel line through $\mathbf{z}$ and find the intersection point with the line through $\mathbf{0}$ and $\mathbf{w'}$. This point is the product of $\mathbf{z}$ and $\mathbf{w}$.

Note. This construction does not work if $\mathbf{0,1,w}$ do not form a triangle, i.e. if $\mathbf{w}$ is on the real line. But in such a case we can swap points and use the first construction.

Algebraic formula

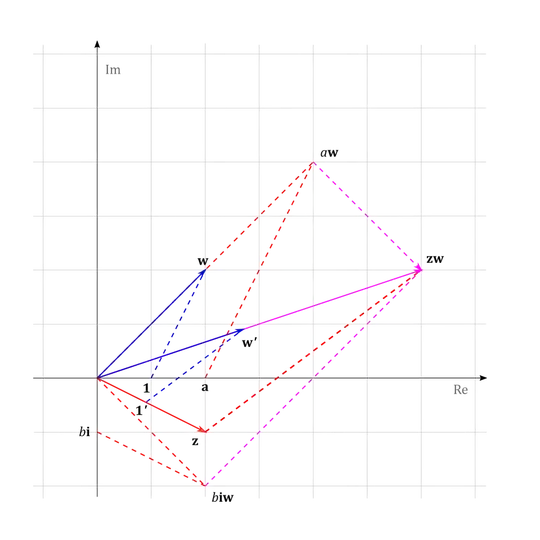
We introduce addition of points (pairs of real numbers) in the usual fashion.

Definition. The sum of $\mathbf{z}$ and $\mathbf{w}$ is a unique point $\mathbf{z} + \mathbf{w}$ such the points $\mathbf{0, z, z+ w, w}$ are the vertices of a parallelogram.

Let's denote by $\mathbf{i}$ the point that is on $Im$-axis at distance one unit from the origin. A point $\mathbf{z}$ can be expressed in terms of its coordinates $\mathbf{z} = a\mathbf{1} + b\mathbf{i}$. We geometrically prove a special case of the distributive property: $\mathbf{z\cdot w}=(a\mathbf{1} + b\mathbf{i}) \cdot \mathbf{w} = a\mathbf{w}+ b\mathbf{i} \cdot \mathbf{w}$.

From the construction of the product $a\mathbf{w}$ it is easy to derive its coordinates as $(ac,ad)$. To obtain coordinates of $b\mathbf{i}\cdot \mathbf{w}$ we note that $\mathbf{1'}=\mathbf{i}$ and $\mathbf{w'}$ is rotated by 90 degrees, so its coordinates are $(-d,c)$. Therefore the coordinates of $b\mathbf{i}\cdot \mathbf{w}$ are $(-bd,bc)$. This and the special case of the distributive property gives as: \begin{align} (a, b) \cdot (c, d) &= (ac, ad) + (-bd,bc) \\ & = (ac - bd, ad + bc). \end{align}

Approach 2

This rationalizes used the fact that complex numbers can be thought as some special transformation of the plane that involve only scaling and rotation (but not reflections) around the origin. If students know some concepts of linear algebra this can be explained fast via a 'change of basis'.

Change of basis.

We start with $\mathbb{R}^2$ treated as a standard vector space over real numbers. We introduce the standard basis: $\mathbf{1}=(1,0)$ $\mathbf{i}=(0,1)$. For any given non zero vector $\mathbf{w}=(c,d)$, we define a new basis vectors $\mathbf{w}=(c,d)$, $\mathbf{w'}=(-d,c)$. We define the product of $\mathbf{z}=(a,b)$ and $\mathbf{w}=(c,d)$ by requiring that the coordinates of $\mathbf{z \cdot w}$ in the basis $(\mathbf{w, w'})$ and of $\mathbf{z}$ in standard basis $(\mathbf{1, i})$ are the same. Using the change of basis formula we can find that the coordinates of $\mathbf{z \cdot w}$ in the standard basis are given by $(\mathbf{w,w'})\mathbf{z}$ where$(\mathbf{w,w'})$ is the change of basis matrix which is the matrix whose columns are the coordinates of the new basis vectors in the standard basis. Alternatively, $\mathbf{z \cdot w}$ is a linear combination $a\mathbf{w}+b\mathbf{w'}$. Either way we get:

$$ \begin{align} (a, b) \cdot (c, d) & = \left(\begin{matrix} c & -d \\ d & c \end{matrix} \right) \left( \begin{matrix} a \\ b \end{matrix} \right) \\ & = (a, b) \left(\begin{matrix} c & d \\ -d & c \end{matrix} \right) \\ & = a(c, d) + b(-d,c) \\ & = (ac - bd, ad + bc). \end{align} $$

If the language of vector spaces is to be avoided then following more lengthy may be used instead of the change of basis approach.

Multiplication of Real Numbers

Let's start by drawing a real line with an fixed origin $\mathbf{0}$ and a point $\mathbf{1}$ that fines a unit of length. Now every real number $a\in \mathbb{R}$ corresponds to a unique point on the line that is $a$ times the unit of length $\mathbf{1}$, i.e. $a\mathbf{1}$. To arrive at a product of $a$ and $b$, let's introduce a new unit of length $\mathbf{b} = b\mathbf{1}$ from the same origin $\mathbf{0}$ and mark the point that is $a$ times the new unit, i.e. $a\mathbf{b}$. If we measure the $a\mathbf{b}$ in term of the original unit $\mathbf{1}$ then we get a certain real number $p$ which is the product of $ab$ i.e. $a\mathbf{b} = (a\cdot b) \mathbf{1}$. In other words, we order to get $ab$ geometrically we take $a$ times $\mathbf{b}$ (or we scale a new unit $\mathbf{b}$ by $a$) and then measure it in terms of a old unit $\mathbf{1}$.

Multiplication of Complex Numbers

Let's draw a Cartesian coordinate system in a plane with an origin $\mathbf{0}$ and the same unit of length on both axes. Let denote by $\mathbf{1}$ (respectively $\mathbf{i}$) the point that is on $Re$-axis (respectively $Im$-axis) at distance one unit from the origin. Now every point in the plane corresponds to a pair of real numbers. We introduce addition of points (pairs of real numbers) in the usual fashion. After this we can represent any point in the plane in terms their coordinates. If a $\mathbf{z}$ has a coordinates $(a, b)$ then it can be now written in terms of units $\mathbf{1}$ and $\mathbf{i}$: $\mathbf{z} = a\mathbf{1} + b\mathbf{i}$. We can think of $\mathbf{z}$ as $\mathbf{1}$ and $\mathbf{i}$ scaled by $a$ and $b$.

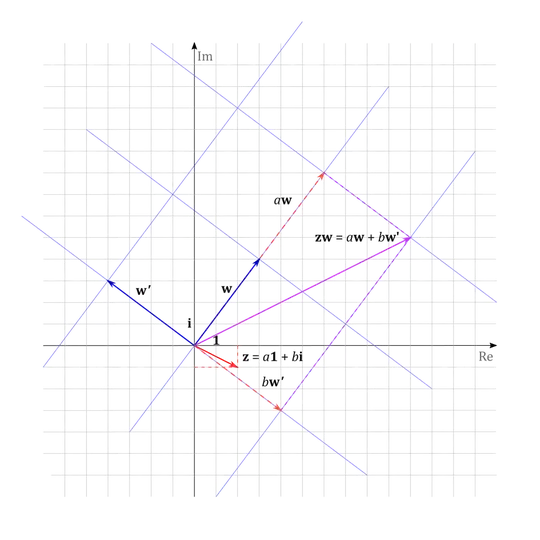
Intuition. Now we would like to define a product of $(a, b)$ and $(c, d)$. Let $\mathbf{z}$ and $\mathbf{w}$ be corresponding points in the plane. The basic idea is to find what a product of $(a, b)$ and $\mathbf{w}$ is first. To do that, we introduce two new units one of them being $\mathbf{w}$ and a second $\mathbf{w'}$ which is somehow related to $\mathbf{w}$ and then to find a point in the plane which scales these new units by $a$ and $b$ respectively i.e. $\mathbf{p} = a\mathbf{w} + b\mathbf{w'}$. The point $\mathbf{p}$ has the same coordinates as $\mathbf{z}$ but in a coordinate system related to $\mathbf{w}$ and $\mathbf{w'}$. Once we measure $\mathbf{p}$ in terms original units $\mathbf{1}$ and $\mathbf{i}$ we will get the coordinates of that point. This will be taken to be the product of $(a, b)$ and $(c, d)$.

Let's go through the process step by step.

Step 1. We have to introduce two new units, for one we take $\mathbf{w}$. In order to obtain a second one, we construct a new Cartesian coordinate system that has the same origin as our original system and we take the point $\mathbf{w}$ to be the new unit at $x$-axis and and define a point $\mathbf{w'}$ that is at the same distance from the origin as $\mathbf{w}$ but on the $y$-axis. The axes of the new system are oriented in the same way as the ones of our original system. The new system can be thought as a scaled and rotated version of the original system obtained is such a way that the unit $\mathbf{1}$ and $\mathbf{i}$ are mapped to $\mathbf{w}$ and $\mathbf{w'}$.

Step 2. We can now find a point $\mathbf{p}$ in the new scaled and rotated Cartesian coordinates that has the coordinates $(a, b)$. Equivalently, we find two points: $a\mathbf{w}$ that is $a$ times $\mathbf{w}$ and another one $b\mathbf{w'}$ that is $b$ times $\mathbf{w'}$. Their sum is $\mathbf{p} = a\mathbf{w} + b\mathbf{w'}$. We take $\mathbf{p}$ to be the product of the points $\mathbf{z}$ and $\mathbf{w}$.

Step 3. We can now find the coordinates of the point $\mathbf{p}=\mathbf{z}\mathbf{w}$ in the terms of the original Cartesian systems, i.e. relate them to $\mathbf{1}$ and $\mathbf{i}$. First, we note that $\mathbf{w'}$ is a rotation of $\mathbf{w}$ by 90 degrees, so its coordinates in the original system are $(-d, c)$, therefore the coordinates of $\mathbf{p}$ can be finally expressed as: $$ a(c, d) + b(-d,c) = (ac - bd, ad + bc).$$

We take this to be a definition of $(a, b) \cdot (c, d)$.

Note. For $\mathbf{z}=a \mathbf{1}$ and $\mathbf{w}= b \mathbf{1}$ the construction delivers the same outcome as for the real numbers.

Answer 3

The complex number (a, b) should actually be a + bi; where $i^2 = -1$.

Therefore, $(a,b) * (c,d) = … = (ac-bd) + (ad+bc)i = (ac-bd, ad+bc)$.