2

Using $f(x)=x^2$ Fourier' series, the proof for $\zeta (2)=\frac{\pi^2}{6}$ is pretty straight forward. I'm wondering if there is a more intuitive explanation for the equality, one that a layman could understand and appreciate.

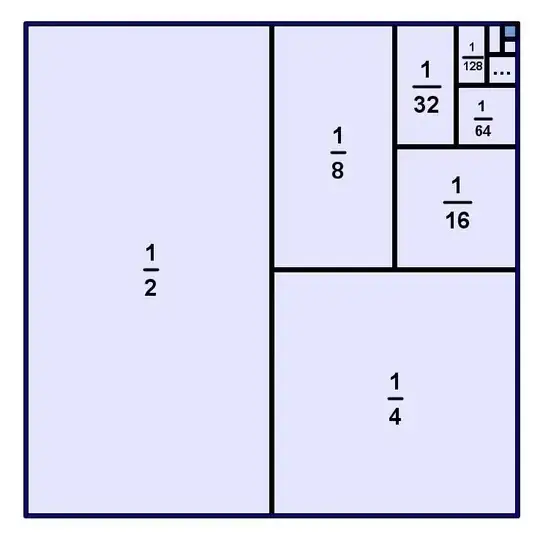
For $\sum_{n=1}^\infty\frac1{2^n}=1$, the intuitive explanation can be given to a 10-year-old, using the following picture enter image description here

Is there a similar intuitive explanation for $\zeta (2)=\frac{\pi^2}{6}$ or $\zeta(2n)$, $n\in \mathbb{N}$ and it's relation to $\pi^2$?

Rasmus Erlemann
  • 2,983
  • 1
    See http://math.stackexchange.com/questions/8337/different-methods-to-compute-sum-limits-n-1-infty-frac1n2. The answer of Hans Lundmark there has a similar picture. – Dietrich Burde Aug 19 '14 at 10:59

0 Answers0