I'm trying to solve $\int{\sin^3(x)\cos^2(x)}dx$.
I got $-\frac{1}{2}\cos(x)+C$, but the memo says $\frac{1}{5}\cos^5(x)-\frac{1}{3}\cos^3(x)+C$
This is my working:
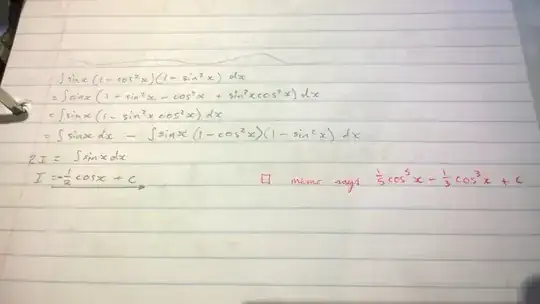
Your help is appreciated!
I'm trying to solve $\int{\sin^3(x)\cos^2(x)}dx$.
I got $-\frac{1}{2}\cos(x)+C$, but the memo says $\frac{1}{5}\cos^5(x)-\frac{1}{3}\cos^3(x)+C$
This is my working:
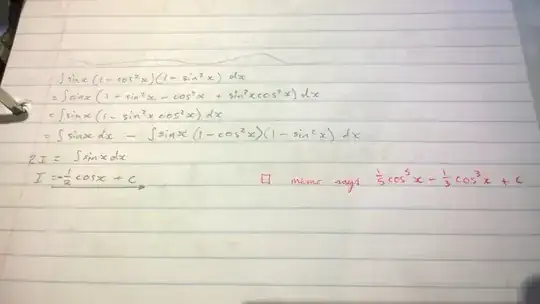
Your help is appreciated!
Rewrite as
$$\int(1-\cos^2 x) \cos^2 x \sin x \ dx$$
and let $t=\cos x\Rightarrow dt = -\sin x \ dx$.
Hint :
It will be easy if you didn't write $\cos^2x$ as $1-\sin^2x$. Write the integrand as $\sin x(1-\cos^2x)\cos^2x$ then set $t=\cos x$.
I was challenged to do this question without using either substitution or even $\sin^2 x + \cos^2x = 1$,
$\sin^3 x \cdot\cos^2 x \\ = \sin x \cdot \sin^2 x \cdot \cos^2 x\\ = \sin x \cdot (\frac{1}{2}\cdot 2\sin x\cdot\cos x)^2\\ = \sin x \cdot (\frac{1}{2} \sin 2x)^2\\ = \frac{1}{4}\cdot (\sin x \cdot \sin 2x) \cdot \sin 2x\\ = \frac{1}{4} \cdot \frac{1}{2} (\cos x - \cos 3x)\cdot \sin 2x\\ = \frac{1}{8}\cdot (\sin2x\cdot \cos x - \sin2x\cdot \cos3x)\\ =\frac{1}{8}\cdot[\frac{1}{2}(\sin x + \sin 3x) - \frac{1}{2}(\sin(-x) + \sin5x) ]\\ =\frac{1}{8}\cdot\frac{1}{2} (\sin x + \sin 3x + \sin x - \sin 5x)\\ =\frac{1}{16}(2\sin x + \sin3x - \sin 5x)\\$
$$\therefore \int{(\sin^3x\cdot\cos^2x)}\cdot dx \\ = \frac{1}{16}\int{(2\sin x + \sin3x - \sin 5x)}\cdot dx\\ = \frac{(-\cos x)}{8} + \frac{(-\cos3x)}{3\times 16} - \frac{(-\cos5x)}{5\times 16} + C\\ = \frac{\cos5x}{80} - \frac{\cos3x}{48} - \frac{\cos x}{8} + C$$
$\dots$which isn't the answer in the memo but that doesn't mean it isn't right.
Now, if there's any math teacher out there who won't accept my answer on a written examination, please speak or forever hold your peace.
This can be rewritten as $ \int \sin^2(x) \cos^2(x) \sin(x) dx $
using the property that $ \sin^2(x) = 1 - \cos^2(x) $, we can rewrite the original integral as
$ \int (1 - \cos^2(x)) \cos^2(x) \sin(x)dx $
substitute $u = \cos(x)$ gets us
$ -\int (1 - u^2)(u^2)du $
= $ -\int u^2 - u^4 du$
now we have an easy integrand to work with:
$ -\int u^2 - u^4 du = -(\frac{u^3}{3} - \frac{u^5}{5} + C) $
= $\frac{u^5}{5} - \frac{u^3}{3} + C$
substitute $ u = \cos(x) $ to obtain the final answer
$\frac{\cos^5(x)}{5} - \frac{cos^3(x)}{3} + C$
Just to comment on your attempted solution (from the picture in your post).
You wrote: $$ \int \sin^3 x \cos^2x\,\mathrm{d}x = \\ \int \sin x (1-\cos^2x)(1-\sin^2x)\,\mathrm{d}x=\\ \int \sin x (1-\cos^2x-\sin^2x+\cos^2x\sin^2x)\,\mathrm{d}x\overset{*}=\\ \int \sin x (1-\cos^2x\sin^2x)\,\mathrm{d}x=\\ \int \sin x \,\mathrm{d}x - \int \sin^3 x \cos^2x\,\mathrm{d}x $$ $2I=\int \sin x \,\mathrm{d}x$ $I=-\frac12\cos x+C$
I think the mistake is in the step marked by $(*)$, where you equated these two things $$1-\cos^2x-\sin^2x+cos^2x\sin^2x \overset{?}= 1-\cos^2x\sin^2x$$ If you plug in $x=0$, you will see that they are not equal. (LHS is equal to 0 for $x=0$ and the RHS is equal to 1.)
This has already been mentioned in comments.