Prove or disprove this calculus limit result by geometric approach

Question

my question is: Could we prove the this conversion of variable work by my formula on the bottom?

$$\iint_R f(r,\theta) \ dxdy = \int_a^b \int_0^{r(\theta)} f(r,\theta) r (dr)\ d\theta$$

as $d r$ and $d \theta$ approach $0$. Prove or disprove that:

$$((r+\Delta r) \cos(a +\Delta \theta) -r \cos a) \cdot ((r+\Delta r) \sin(a + \Delta \theta) -r \sin a) / (r \;\Delta \theta \; \Delta r)=1 .$$ where the variable represent as in this graph :

as $\Delta r $ and $\Delta \theta$ approach $0$

This question is inspired from $dx\;dy=r \;dr \;d \theta$.

Answer 1

The diagram that you are giving is not what is going on at all. $\mathrm{d}x\;\mathrm{d}y$ is an element of area intended to represent the plane broken up into small rectangles.:

$\mathrm{d}r\;\mathrm{d}\theta$ is an element of area in a space whose small squares get mapped to small annular wedges by $x=r\cos(\theta)$, $y=r\sin(\theta)$:

The Jacobian is the matrix that locally maps between two coordinate systems. $$ \frac{\partial(x,y)}{\partial(u,v)}=\begin{bmatrix}\frac{\partial x}{\partial u}&\frac{\partial y}{\partial u}\\\frac{\partial x}{\partial v}&\frac{\partial y}{\partial v}\end{bmatrix}\tag{1} $$ From polar to rectangular coordinates, the Jacobian is $$ \frac{\partial(x,y)}{\partial(r,\theta)}=\begin{bmatrix}\cos(\theta)&\sin(\theta)\\-r\sin(\theta)&r\cos(\theta)\end{bmatrix}\tag{2} $$ Note that $\begin{vmatrix}\cos(\theta)&\sin(\theta)\\-r\sin(\theta)&r\cos(\theta)\end{vmatrix}=r$.

A small area in $\mathrm{d}r\;\mathrm{d}\theta$, the green square, is mapped by the polar coordinate map to the blue annular wedge, which has approximately the same area as the red rectangle. The Jacobian matrix maps the green square to the red rectangle. The ratio of the area of the red rectangle to the green square is the determinant of the Jacobian (this is just linear algebra).

Therefore, since a small square in $\mathrm{d}r\;\mathrm{d}\theta$ is mapped by the coordinate transform so that its area is $\left|\frac{\partial(x,y)}{\partial(r,\theta)}\right|\;\mathrm{d}r\;\mathrm{d}\theta$ $$ \begin{align} \iint f(x,y)\;\mathrm{d}x\;\mathrm{d}y &=\iint f(r,\theta)\left|\frac{\partial(x,y)}{\partial(r,\theta)}\right|\;\mathrm{d}r\;\mathrm{d}\theta\\ &=\iint f(r,\theta)\;r\;\mathrm{d}r\;\mathrm{d}\theta\tag{3} \end{align} $$

Answer 2

I've understood your question as the question whether $$\lim\limits_{\substack{\Delta r\to 0\\\Delta a\to 0}} \frac{((r+\Delta r) \cos(a +\Delta \theta) -r \cos a) \cdot ((r+\Delta r) \sin(a + \Delta \theta) -r \sin a)}{r \;\Delta \theta \; \Delta r}=1.$$ I hope this was correct.

---

The expression you're asking about has the form $[f(a+\Delta a,r+\Delta r)-f(a,r)]\cdot[g(a+\Delta a,r+\Delta r)-g(a,r)]$ for the functions $$f(a,r)=r\cos a$$ $$g(a,r)=r\sin a$$

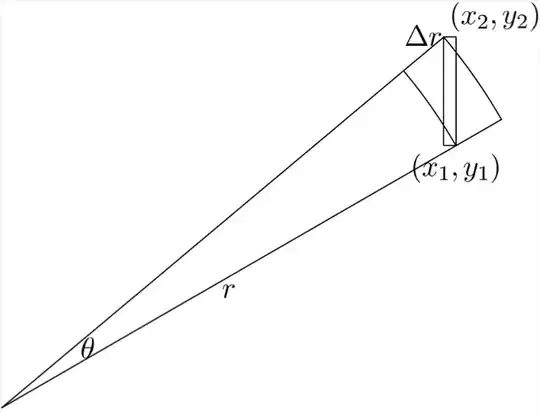
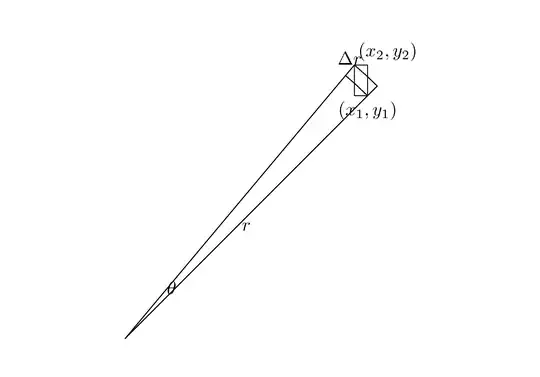
The following picture should show what this expression represents. (With $(x_1,y_1)=(r\cos a,r\sin a)$ and $(x_2,y_2)$ the same for $r+\Delta r$ and $a+\Delta a$, the given expression is just the are of rectangle in the picture.)

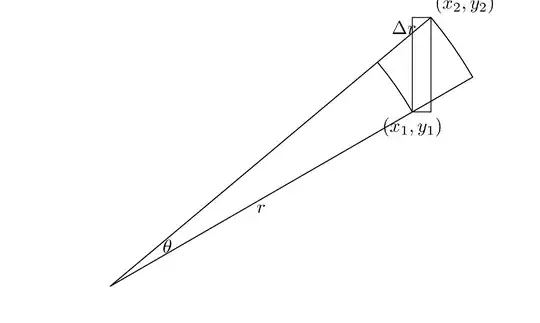
The partial derivatives of these functions are $f_r(a,r)=\cos a$, $f_a(a,r)=-r\sin a$, $g_r(a,r)=\sin a$, $g_a(a,r)=r\cos a$.

Using the first order Taylor polynomial we can approximate this expression as $$(\cos a \Delta r-r\sin a\Delta a)(\sin a\Delta r+r\cos a\Delta a)=$$ $$\cos a\sin a (\Delta r)^2 + r(\cos^2a-\sin^2a) \Delta a \Delta r - r^2 \sin a \cos a (\Delta a)^2.$$

---

Let us check at lest in some special cases whether we get what we would expect.

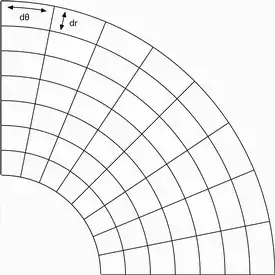
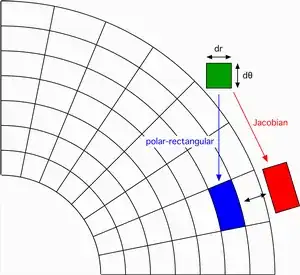
If $a\approx 0$, then the above expression is close to $r\Delta a\Delta r$. From the following figures we see, that we would really expect it to approximate quite well the area between the two arcs.

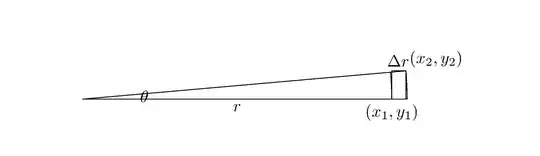
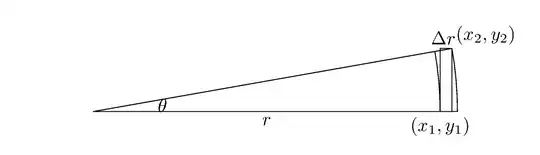
But for $\cos a=\sin a = \frac{\sqrt 2}2$ this expression is approximately $\frac{(\Delta r)^2}2-r^2\sin a\cos a(\Delta a)^2$. The following picture show that it can really attain positive values, values close to zero, and negative values.

---

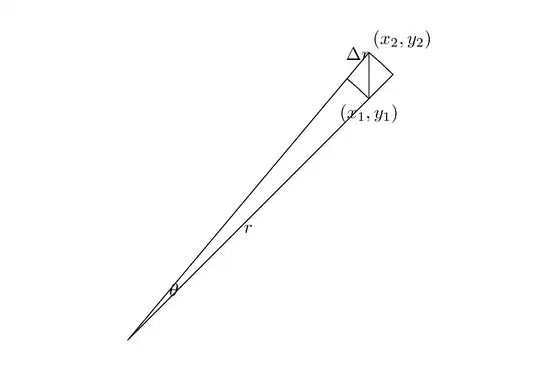
I am sorry for the large size of the pictures - obviously I am not too good in converting graphics. If someone would like to see the metapost source, it is available here.

Adding an explanation in order to capture intuition behind the above computations.

First let us work with only one variable and with a differentiable functions $h(x)$. The definition of the derivative says that $$\lim\limits_{\Delta x\to 0} \frac{h(x_0+\Delta x)-h(x_0)}{\Delta x}=h'(x_0),$$ i.e. derivative is the number such that $\frac{h(x_0+\Delta x)-h(x_0)}{\Delta x_0} \approx h'(x_0)$ for small $\Delta x$. In other words, if we replace $h(x)$ by a linear function $h(x) \approx h(x_0)+h'(x_0)(x-x_0) =h(x_0)+h'(x_0)\Delta x$, then we do not make too big mistake. For more precise introduction what it means that the mistake is not "too big" see e.g. wikipedia article or your favorite analysis textbook.

Note that the above can be rewritten as $h(x)-h(x_0) \approx h'(x_0)\Delta x$.

Taylor's theorem in two variables is slightly more complicated, but the basic idea is the same. We approximate the function by a linear function. In two dimension this is not a line but a plane. For nice functions (with enough continuous partial derivatives) it can be again shown that mistake will not be "too big".

Partial derivatives are precisely derivatives in the direction parallel to axes. So in two dimension the tangent plane is given by the equation $$h(x,y)-h(x_0,y_0) \approx \frac{\partial h}{\partial x}(x_0,y_0) \Delta x + \frac{\partial h}{\partial y}(x_0,y_0) \Delta y,$$ where $\Delta x=x-x_0$, $\Delta y=y-y_0$.

---

Perhaps some other questions on this site can be useful in getting intuition about Taylor's polynomial in several variables, e.g.:

• Multivariate Taylor Series Derivation (2D)

• What is the vector form of Taylor's Theorem?