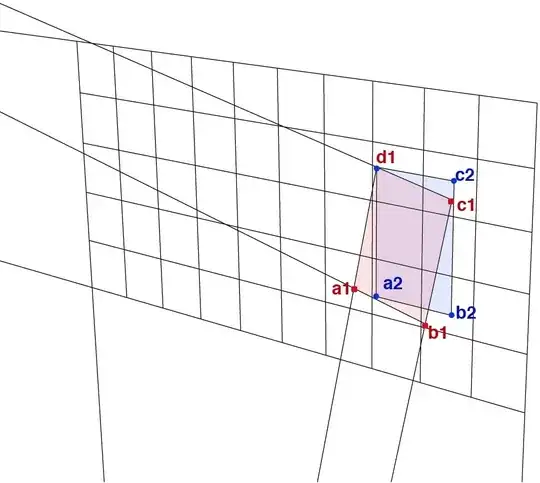
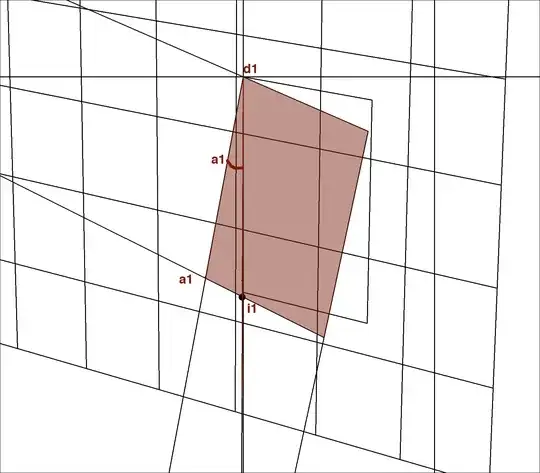
all though only the 2D data is available, the best way to think of this problem is a piece of paper pinned at one corner to a wall, but the paper is sitting at an angle to the wall, see illustration below, this generates a second set of vanishing points v2a and v2b. Given only this 2D data, I want to rotate the "paper" so it is parallel to the wall, which is easy enough to rotate, but point a1 stretches out to a new length d1-a2, this does not stretch proportionately with the length of v2b going to v1b, because it is in perspective (from a 3D world), it is instead some log proportion.
so this is the question, what is the calculation that is used to find the new length d1-a2? after a rotation as shown, given a known length d1-a1 (in a 2dimensional set up as shown).
I am not very good at reading scientific notation, so if the answer could also be expressed in "C" or objective-C code, (or even sudo code) that would be great.