When $\theta$ is very small, why is sin $\theta$ taken to be JUST $\theta$?
Asked
Active
Viewed 7,295 times
4
-
2We have that $\lim_{x\to0}\frac{\sin x}x=1$ so that $\sin x$ is close to $x$ when $x$ is small. – Cm7F7Bb Aug 12 '14 at 11:40
-
Put your calculator in radian mode. Calculate $\sin\theta$ for various smallish $\theta$. You will be impressed by how close it is to $\theta$. – André Nicolas Aug 12 '14 at 11:44
-
1$x-\frac{x^3}{6}<\sin x < x$ when $x$ is small. – Thomas Andrews Aug 12 '14 at 11:45
-
This is only true when the angle is measured in radians. Radians are defined for the sake of making the statement true. – DanielV Aug 12 '14 at 12:22
-
here θ is in radian or degrees?for this rule/principle? – DSP_CS Dec 17 '20 at 16:51
2 Answers
12
It's not just $\theta$.
What you observe is the fact that $\sin \theta$ and $\theta$ approach zero from either side of the number line at a pretty similar rate. This can be best demonstrated with a graph.
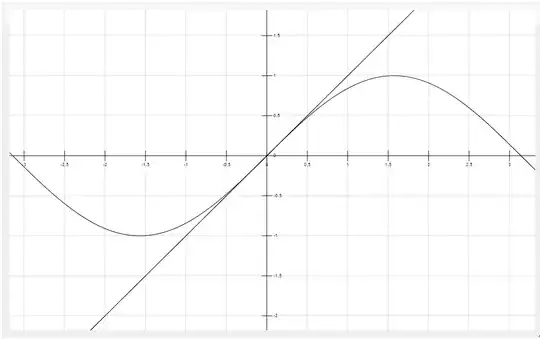
You can see that they are about to overlap just at zero. So when $\sin \theta$ is approaching $0$ for some very very small $\theta$ we can approximate it as $\theta$.
Does this make sense?
Ali Caglayan
- 5,726
1
=== Geometric ===
.
The red section on the right, d, is the difference between the lengths of the hypotenuse, H, and the adjacent side, A. As is shown, H and A are almost the same length, meaning cos θ is close to 1 and $\theta^2/2$ helps trim the red away. :
$\cos{\theta} \approx 1 - \frac{\theta^2}{2}$
The opposite leg, O, is approximately equal to the length of the blue arc, s. Gathering facts from geometry, s = A*θ, from trigonometry, sin θ = O/H and tan θ = O/A, and from the picture, $ O \approx s $ and $ H \approx A $ leads to:
:$\sin \theta = {O\over H}\approx{O\over A} = \tan \theta = {O\over A} \approx {s\over A} = {{A*\theta}\over A} = \theta$.
Simplifying leaves,
:$\sin \theta \approx \tan \theta \approx \theta$.
