How do I solve $\vert x\vert^{x^2-2x} = 1$?

Question

I have the exponential equation $\vert x\vert^{x^2-2x} = 1$, but how do I solve it?

Answer 1

Either $x = \pm 1$ (so the value of the exponent doesn't really matter)

Or $x^2 -2x = 0$ but $x \neq 0$ i.e. $x = 2$ (any non-zero number to the zero-th power is one)

Answer 2

Hint:

note that your equation is equivalent to:

$$(x^2 - 2x) \, \log{|x|} = 0,$$ what can we say about a product of two factors if it is equal to zero?

---

Edit:

Suggested by @CDspace, here's a plot of $f(x) = |x|^{x^2-2x} - 1$ where we can visually see the solutions of $f(x) = 0$:

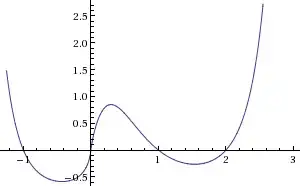
Pretty cool!

Answer 3

I believe $x=0$ is a solution, because $x^x$ is continuous as $x$ approaches $0$. Consider $\lim_{x \to 0}x^x$. Let $$f(x_n)=\bigg(\frac{1}{x}\bigg)^{\frac{1}{x}}$$such that $$ y=\bigg(\frac{1}{x}\bigg)^{\frac{1}{x}} $$Then $$ ln(y)=\frac{1}{x}ln\bigg(\frac{1}{x}\bigg)=\frac{1}{x}(ln1-lnx)=\frac{1}{x}(0-lnx)=-\frac{lnx}{x} $$Now, using L'Hopital's rule, $$ \lim_{x\to\infty}\bigg(-\frac{lnx}{x}\bigg)=\lim_{x\to\infty}\bigg(-\frac{\frac{1}{x}}{1}\bigg)=\lim_{x\to\infty}\bigg(-\frac{1}{x}\bigg)=0 $$ Now, $$ \lim_{x\to\infty}f(x_n)=\lim_{x\to\infty}y=\lim_{x\to\infty}e^{lny}=\lim_{x\to\infty}e^{-\frac{1}{x}}=e^0=1 $$Therefore, $$ 0^0=\lim_{x\to 0}x^x=\lim_{x\to 0}f(x)=\lim_{x\to\infty}f(x_n)=1 $$The solutions given by the graph provided by @CDspace are therefore correct: {-1,0,1,2}