What we can say about $(-\sqrt{2})^{(-\sqrt{2})^{(-\sqrt{2})^\ldots}}$?

Question

Problem:

How we can strictly prove $(-\sqrt{2})^{(-\sqrt{2})^{(-\sqrt{2})^\ldots}}$ can't be 2?

Can $(-\sqrt{2})^{(-\sqrt{2})^{(-\sqrt{2})^\ldots}}$ have the value expressed by complex numbers? (See below, in calculation details), like $i^i=e^{-\frac{\pi }{2}+2k\pi} \quad (k \in \mathbb{Z})$?

Details:

In this other question of mine, Are the solutions of $x^{x^{x^{x^{\cdot^{{\cdot}^{\cdot}}}}}}=2$ correct?, I show how to find the possible solutions for $x$ in the equation. $\sqrt{2}$ is one root and this is ok, but, what about $-\sqrt{2}$? Maybe it isn't a root, but how to strictly prove this? The prove given in that question (as we can read in the comments) looks wrong, so I'm searching for a correct one.

Calculation details

This was posted in the other question (as an answer, but the truth is just a huge comment, as I explained) and I think is pertinent to here too.

" It looks like $-\sqrt{2}$ isn't a solution for the equation, but I'm not sure. Looks like too, the power tower of a number should converge only on a specific interval ($[e^{−e},e^{1/e}]$).

But using Mathematica and the ProductLog function (the Lambert $W(z)$ function) we find some strange things:

Using $h(z)=z^{z^{z^{\ldots}}}=-\frac{W(-\log (z))}{\log (z)}$ (h[z_]:=(-ProductLog[-Log[z]])/Log[z])

Calculating the power tower to $\sqrt{2}$ we have N[h[Sqrt[2]], 10]=2.000000000

And the power tower to $-\sqrt{2}$ we have N[h[-Sqrt[2]], 10]=0.2513502988 + 0.3162499180 I

Calculating explicity, by iteration

${-\sqrt{2}},{(-\sqrt{2})}^{({-\sqrt{2}})},{(-\sqrt{2})}^{({-\sqrt{2})}^{\ldots}}$ we have

Table[N[Re[PowerTower[-Sqrt[2], i]], 30] + I*N[Im[PowerTower[-Sqrt[2], i]], 5], {i, 1, 15}] // TableForm

-1.41421356237309504880168872421
-0.163093997943414854921937604558+0.59044 I
 0.140921295793052749536215801866-0.044791 I
 1.10008630700672531426983704055+0.50079 I
-0.268168781568546776692908102136-0.14235 I
 0.894980750563013739735614892750-1.1090 I
-33.5835630157562847787187418023+29.118 I
 6.49187847255812829134661655850*10^-46-1.5181*10^-45 I
 1.00000000000000000000000000000+1.5134*10^-45 I
-1.41421356237309504880168872421-2.2930*10^-44 I
-0.163093997943414854921937604558+0.59044 I
 0.140921295793052749536215801866-0.044791 I
 1.10008630700672531426983704055+0.50079 I
-0.268168781568546776692908102136-0.14235 I
 0.894980750563013739735614892750-1.1090 I

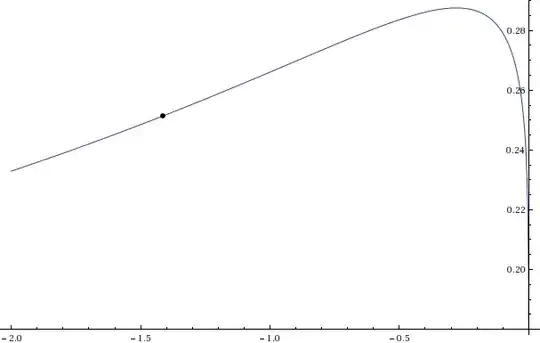
Plotting the real and imaginary part of the function $h$, we have:

To the real part:

Plot[Re[N[h[x]], {x, -2, 0}, Epilog -> {PointSize[0.01], Point[{-Sqrt[2], N[Re[h[-Sqrt[2]]]]}]}]

Real part of the tower of -Sqrt2

and to the imaginary part:

Plot[Im[N[h[x]], {x, -2, 0}, Epilog -> {PointSize[0.01], Point[{-Sqrt[2], N[Im[h[-Sqrt[2]]]]}]}]

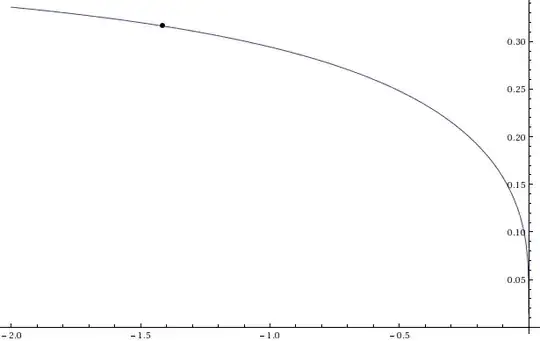
Imaginary part of the tower of -Sqrt2

So looks like the function converges, but, unfortunately not to $2$.

"

Taking the principal value of the exponentials ... 8 steps is very close to zero. Around $10^{-45}$. Then 9 steps is close to 1, and then at 10 starts over again. So if you are doing this numerically, you had better take many more than 45 places in your approximations! — GEdgar, Dec 07 '11 at 22:35
@GEdgar, unfortunally the computer couldn't calculated much more =// . If you can generate some other values, please post here ^^. — GarouDan, Dec 07 '11 at 22:48
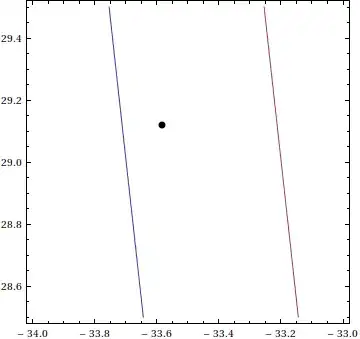
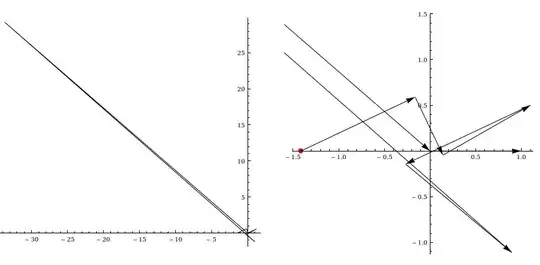
The iteration looks pretty chaotic. Try Graphics[{AbsolutePointSize[2], Line[Composition[Through, {Re, Im}] /@ Drop[NestList[((-Sqrt[2])^#) &, N[-Sqrt[2], 100], 600], 150]]}, Axes -> True, PlotRange -> {{-5/2, 5/2}, {-5/2, 5/2}}] — J. M. ain't a mathematician, Dec 08 '11 at 01:55
Raising a negative number (or any complex number that is not a positive real) to a non-integer power is not a well-defined thing to do. The basic example is $(-1)^{1/2}$. Is that $i$ or $-i$? It just gets worse with irrational powers. $-\sqrt{2}^{-\sqrt{2}}$ could be interpreted as $\sqrt{2}\exp(-\pi i\sqrt{2})$, $\sqrt{2}\exp(-3\pi i\sqrt{2})$, $\sqrt{2}\exp(-5\pi i\sqrt{2})$, etc. and all of these are different. You might decide to enforce that all arguments always be reduced to values in $(-\pi,\pi]$, but that would be unnatural and give discontinuous operations. — 2'5 9'2, Dec 08 '11 at 05:02
Using the branches of the lambert-w we get ~2 for the first negative branch (http://www.wolframalpha.com/input/?i=-W%28-1%2C-log%28-sqrt%282%29%29%29%2Flog%28-sqrt%282%29%29) and ~4 for the second negative branch (http://www.wolframalpha.com/input/?i=-W%28-2%2C-log%28-sqrt%282%29%29%29%2Flog%28-sqrt%282%29%29). Both fixpoints are repelling, so we approximate them only by the iteration of the inverse operation $\small x_{j+1}=(\log(x_j)+k2 \pi i)/\log(b) $ where $\small b=-\sqrt2$ for k=-1* and k=-2 — Gottfried Helms, Dec 08 '11 at 07:59
Yes, you're right @alex.jordan. But as I explain in the question, maybe this tetration looks like something like $i^i=e^{-\frac{\pi }{2}+2k\pi} \quad (k \in \mathbb{Z})$. — GarouDan, Dec 09 '11 at 22:33
@GottfriedHelms, lol. Interesting thing, could this show the number converge to $2$ too? Maybe it converges to $2$ and several another ones. (I'm not afilliated to this $k=-1$ and $k=-2$, so I need see this a little). — GarouDan, Dec 09 '11 at 22:37
@GarouDan: :-) No, the "attracting" one is the 9-period-orbit. But for the inverse operation (the log) and the multiple branches of the log there are infinitely many fixpoints, such that $\small \log(x_0)/log(b)=x_0$ which may be called the k=0'th fixpoint (at x_0). The other k'th fixpoints are defined by $ \small (\log(x_k)+ k \cdot 2 \pi i )/log(b)=x_k$ and are "attracting" for that log-operations (try the iteration with some initial value). These k define the branches for the loag as well as for the lambert-w-function. This is all more obvious if the other direction of indexing is used. — Gottfried Helms, Dec 09 '11 at 22:57
@GarouDan I think that's my point. If you raise a general complex number to a general complex power (as in $i^i$) there are infinitely many interpretations of the result ($\ldots\exp(-\pi/2), \exp(3\pi/2), \ldots$), and none of them are canonical. $(-\sqrt2)^{-\sqrt{2}}$ has the same problem. How do you choose which representative from ${\sqrt2^{-\sqrt2}\left(\cos(\sqrt{2}(\pi+2\pi k))-i\sin(\sqrt{2}(\pi+2\pi k))\right)}$ to continue working with? Because they are all different. — 2'5 9'2, Dec 10 '11 at 00:04
Did you mean $$(-\sqrt{2})^{ (-\sqrt{2})^{\cdots}} $$ or $$-\left( \sqrt{2}^{- \left(\sqrt{2}^{-\left( \cdots \right)} \right)} \right)$$ — , Feb 24 '13 at 03:23
@GarouDan how can we figure about some initial value of $a$ and $b$ where $a+bi$ is your $(-\sqrt{2})^{ (-\sqrt{2})^{\cdots}}$? — Shivam Patel, May 25 '14 at 10:38

Gottfried Helms · Answer 1 · 2011-12-08T04:57:18.883

This is the list of the absolute values of the iterates of $\small b=-\sqrt{2} $ . Because it has a very obvious 9-periodic pattern at the beginning I separated the trajectory in vertical columns of only 9 subsequent iterates. (computed with Pari/GP, internal precision 1200 decimal digits)

$$ \Tiny \begin{array} {rrrr} 1.4142136 & 1.4142136 & 1.4142136 & 1.4142136 & 1.4142136 \\ 0.61254733 & 0.61254733 & 0.61254733 & 0.61254733 & 0.61254733 \\ 0.14786831 & 0.14786831 & 0.14786831 & 0.14786831 & 0.14786831 \\ 1.2087108 & 1.2087108 & 1.2087108 & 1.2087108 & 1.2087108 \\ 0.30360689 & 0.30360689 & 0.30360689 & 0.30360689 & 0.30360689 \\ 1.4251197 & 1.4251197 & 1.4251197 & 1.4251197 & 1.4251197 \\ 44.448758 & 44.448758 & 44.448758 & 44.448758 & 44.448758 \\ 1.6510623E-45 & 1.6510623E-45 & 1.6510623E-45 & 1.6510623E-45 & 1.6510623E-45 \\ 1.0000000 & 1.0000000 & 1.0000000 & 1.0000000 & 1.0000000 \end{array} $$ And here are the first-order differences between subsequent columns. We see, that the differences vanish quickly so this indicates strongly a convergence to a 9-period-fixpoint structure for the lenghtes: $$ \Tiny \begin{array} {rrrr} 1.4142136 & -4.2758815E-45 & 1.5415076E-84 & -3.5904308E-124 & 7.0561983E-164 \\ 0.61254733 & 4.5034171E-44 & -6.6081983E-84 & 8.9967024E-124 & -1.1106139E-163 \\ 0.14786831 & -2.0529932E-44 & 2.8802422E-84 & -3.7054357E-124 & 4.1945575E-164 \\ 1.2087108 & -1.4713104E-44 & -9.1472657E-85 & 6.2615464E-124 & -1.6552948E-163 \\ 0.30360689 & 7.6680831E-44 & -1.1071058E-83 & 1.4777436E-123 & -1.7723010E-163 \\ 1.4251197 & 1.7072251E-43 & -3.7497694E-83 & 7.1363187E-123 & -1.2382368E-162 \\ 44.448758 & 4.3205739E-41 & -7.3721684E-81 & 1.1721448E-120 & -1.7432962E-160 \\ 1.6510623E-45 & -2.4711650E-85 & 3.4434076E-125 & -4.3898227E-165 & 4.8945927E-205 \\ 1.0000000 & -6.8798480E-85 & 8.6346349E-125 & -9.3717918E-165 & 7.3761858E-205 \end{array} $$

This is the same with the arg (angle in the complex plane) of the iterates: $$ \Tiny \begin{array} {rrrr} 3.1415927 & -3.1415927 & -3.1415927 & -3.1415927 & -3.1415927 \\ 1.8403024 & 1.8403024 & 1.8403024 & 1.8403024 & 1.8403024 \\ -0.30774541 & -0.30774541 & -0.30774541 & -0.30774541 & -0.30774541 \\ 0.42719397 & 0.42719397 & 0.42719397 & 0.42719397 & 0.42719397 \\ -2.6536012 & -2.6536012 & -2.6536012 & -2.6536012 & -2.6536012 \\ -0.89181076 & -0.89181076 & -0.89181076 & -0.89181076 & -0.89181076 \\ 2.4273000 & 2.4273000 & 2.4273000 & 2.4273000 & 2.4273000 \\ -1.1666935 & -1.1666935 & -1.1666935 & -1.1666935 & -1.1666935 \\ 1.5133579E-45 & 1.5133579E-45 & 1.5133579E-45 & 1.5133579E-45 & 1.5133579E-45 \end{array} $$ and the differences $$\Tiny \begin{array} {rrrr} 3.1415927 & -6.2831853 & -2.3079194E-84 & 3.0257404E-124 & -3.5304957E-164 \\ 1.8403024 & 5.4860495E-45 & -3.7116105E-84 & 9.7966678E-124 & -2.0437302E-163 \\ -0.30774541 & -3.3111505E-44 & 1.0414472E-83 & -2.3245643E-123 & 4.4644292E-163 \\ 0.42719397 & -6.5587742E-44 & 1.0295176E-83 & -1.5111378E-123 & 2.0580665E-163 \\ -2.6536012 & 3.4000673E-44 & -1.5018863E-83 & 3.6815608E-123 & -7.4238709E-163 \\ -0.89181076 & -2.1319630E-43 & 2.7199457E-83 & -3.0364896E-123 & 2.5759836E-163 \\ 2.4273000 & -5.1815970E-43 & 3.9336883E-83 & 6.3329419E-124 & -1.1315814E-162 \\ -1.1666935 & -3.9316194E-41 & 1.1769005E-80 & -2.5814484E-120 & 4.9090189E-160 \\ 1.5133579E-45 & -4.2285808E-85 & 9.0338626E-125 & -1.6915902E-164 & 2.9002867E-204 \end{array} $$ Again we see, that they vanish quickly and since the angles and the lengthes (absolute values) seem to approximate 9 values its a good hypothese, that this is 9-periodic fixpoints.

The mean of the fixpoints is then approximately $\small m_\infty = -3.5881168+3.2125197*I $

@GarouDan The way I feel with this guy's post. Man, lengthy and rich. — Simply Beautiful Art, Dec 22 '16 at 18:32

score 3 · Answer 2 · answered Dec 08 '11 at 01:33

From Maple: Let $x[1] = -\sqrt{2}$ and $x[n+1] = (-\sqrt{2})^{x[n]}$. Some numerical results using the principal value for the exponentials.

x[  1] = -1.414213562373095048801688724209698078569671875376948073176679737990732
    +0.000000000000000000000000000000000000000000000000000000000000000000000 i

x[  2] = -0.163093997943414854921937604558017962499793965727869386822402042154175
        +0.590435919538534820623115985186637206577707103759559066773060672459998 i

x[  3] = 0.140921295793052749536215801866147804169595017211147358356211625506612
        -0.044790898341731398052941928863585335872205418214802335628821017645623 i

x[  4] = 1.100086307006725314269837040545062800076092484472530604917053566055528
        +0.500791346054036352743920991367697779027338760297890701264222550336166 i

x[  5] = -0.268168781568546776692908102135608983545959166888483749205191974796848
        -0.142346920553878866119517412480250679122455204231360202301605215735912 i

x[  6] = 0.894980750563013739735614892750496547408631351459698268792989443758413
        -1.109042679617501408669836777920686914041610008570543149982061855745641 i

x[  7] = -33.583563015756284778718741802267673776552912769626319413100735640780956
        +29.117630558936738895309311011584496358235358548332430845036010574467116 i

x[  8] = 0.000000000000000000000000000000000000000000000649187847255812829134662
        -0.000000000000000000000000000000000000000000001518078385198129994507332 i

x[  9] = 1.000000000000000000000000000000000000000000004994175265501475052691346
        +0.000000000000000000000000000000000000000000001513357895454095189313419 i

x[ 10] = -1.414213562373095048801688724209698078569671871101066587094934996112240
        -0.000000000000000000000000000000000000000000022930276777769681861169385 i

x[ 11] = -0.163093997943414854921937604558017962499793980957618715410603002901938
        +0.590435919538534820623115985186637206577707146273368937624772962839578 i

and evidence of periodicity...

x[  1] = -1.414213562373095048801688724209698078569671875376948073176679737990732478462107038850387534327641573
        +0.000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 i
x[ 10] = -1.414213562373095048801688724209698078569671871101066587094934996112240314574971797998806072494141208
        -0.000000000000000000000000000000000000000000022930276777769681861169384867946447483376541158075718190 i
x[ 19] = -1.414213562373095048801688724209698078569671871101066587094934996112240314574971798000347580082307702
        -0.000000000000000000000000000000000000000000022930276777769681861169384867946447483373277267119819928 i
x[ 28] = -1.414213562373095048801688724209698078569671871101066587094934996112240314574971798000347580082307702
        -0.000000000000000000000000000000000000000000022930276777769681861169384867946447483373277267119819928 i

GEdgar, I'll take a look and return. Thx. – GarouDan Dec 09 '11 at 22:39 — GarouDan, Dec 09 '11 at 22:39

J. M. ain't a mathematician · Answer 3 · 2011-12-10T10:44:45.527

This is more of an extended comment, but I'll leave it here and maybe flesh it out later to a full answer if I can figure out more from this.

I managed to confirm the 9-cycle for the iteration $x_{k+1}=(-\sqrt2)^{x_k}$ by using Floyd's cycle finding algorithm.

Here's a Mathematica implementation (adapted from here):

Options[CycleFixedPoint] = {SameTest -> SameQ, CycleTest -> SameQ, 
                            IterationCount -> False};

CycleFixedPoint[f_, start_, opts___] := 
   Block[{nth, twonth, counter, result, value, sameTest, cycleTest, 
         iterationCount},

         {sameTest, cycleTest, iterationCount} =
         {SameTest, CycleTest, IterationCount} /. {opts} /.
          Options[CycleFixedPoint];

         nth = f[start]; twonth = f[f[start]]; counter = 1;

         While[(! sameTest[nth, twonth]) && (counter < $IterationLimit), 
               nth = f[nth]; twonth = f[f[twonth]]; ++counter;]

         If[counter == $IterationLimit, result = nth,
            (* else *)
            value = f[nth];
            result = Prepend[Flatten[Last[
                             Reap[While[! cycleTest[value, nth],
                                        Sow[value]; value = f[value];
                                  ]]
                             ], 1], nth]
            ];

         If[TrueQ[iterationCount], {result, counter}, result]
         ]

Using 120 significant digits, I executed Short[AbsoluteTiming[{cycle, count} = CycleFixedPoint[((-Sqrt[2])^#) &, N[-Sqrt[2], 120], IterationCount -> True]]] to find the 9-cycle. Here is the cycle I found to fifty digits:

-1.41421356237309504880168872420969807856967187110107

-0.16309399794341485492193760455801796249979398095762 +
 0.59043591953853482062311598518663720657770714627337 i

 0.14092129579305274953621580186614780416959499616264 - 
 0.04479089834173139805294192886358533587220541666218 i

 1.10008630700672531426983704054506280007609250392744 + 
 0.50079134605403635274392099136769777902733868204980 i

-0.26816878156854677669290810213560898354595922977896 - 
 0.14234692055387886611951741248025067912245524930130 i

 0.8949807505630137397356148927504965474086312222303 - 
 1.1090426796175014086698367779206869140416103322351 i

-33.583563015756284778718741802267673776552930326435 + 
 29.117630558936738895309311011584496358235404253331 i

 6.491878472558128291346616558500415541158598093491 * 10^(-46) - 
 1.5180783851981299945073316151972156311102228546016 * 10^(-45) i

 1.00000000000000000000000000000000000000000000499418 +
 1.5133578954540951893134194357192492465553697834027 * 10^(-45) i

It does look as if the eighth member isn't zero; a plot of the curves $\Re((-\sqrt 2)^{x+iy})=0$ and $\Im((-\sqrt 2)^{x+iy})=0$ in the vicinity of the seventh member of the cycle gives a strong hint:

is that a zero I see?

(An analytical proof of this will still be needed, though.)

Here are plots of the complex plane trajectory. Since the seventh member of the cycle is a bit larger in magnitude than the others, I have also thrown in a close-up:

power tower trajectory

This paper by Galidakis seems to give some conditions for a power tower iteration (see page 990 for instance), but I seem to have some difficulty applying his criterion for determining the cycle length of the power tower iteration. It involves a multivariate generalization of the Lambert function which Mathematica doesn't have, so I'll need to study this a bit more and see if Galidakis's results can be adapted for this situation.

Hmm, concerning the exactness of fp at 0 and 1: no, the small deviation from the integers remains. Consider the 9-fold iteration by the function $\small x_{k+1}=it9(x_k) $ then the first-order difference d1 between $\small x_0=1 \qquad x_1=it9(x_0) \qquad d_1=x_1-x_0 $ is in the near of 1e-40 and from this the next iteration moves only by about 1e-80 and from this only about 1e-120 and so on. That quality of approximation is suprisingly nearly geometrical; the quotient between subsequent differences goes quickly to a constant near a value of again something like 1e-40. (...cont...) — Gottfried Helms, Dec 10 '11 at 09:09
(...cont...) so possibly (this is only a speculation!) one can implement an acceleration of approximation when that geometric rate (with approximate quotient q) could somehow be inserted by the closed-form of the geometric series using (1-q) in the denominator of some improved formula... — Gottfried Helms, Dec 10 '11 at 09:12
This is something curious. Define the function $\small it9(x) = for(k=1,9,x=\exp(blx));return(x) \qquad \text{ where } bl=\log(-sqrt(2)) $. Then, using Pari/GP, one can ask for the power series of $\small it9(x-1) $ . We get $ \displaystyle it9(x-1) = (0.140921295793 - 0.0447908983417I) + (0.E-1821552 + 0.E-1821552I)x + \ldots $ where all following coefficients are machine-epsilon. Surprisingly the constant is the 4'th or 5'th iterate of $\small x_{k+1}=exp(bl*x_{k})$ beginning at $\small x_0=0 $. Perhaps this helps for focusing the analytical reasoning? — Gottfried Helms, Dec 10 '11 at 22:05

score 2 · Answer 4 · answered May 04 '18 at 11:27

Real solutions: $\enspace x\in\{2;4\}$

Complex solutions: $\enspace\displaystyle x=\frac{W_n(-i\pi - \ln\sqrt{2})}{-i\pi - \ln \sqrt{2}} \enspace$ for $\enspace n\in\mathbb{Z}\enspace$ where $\,W_n\,$ is the analytic

continuation of the product log function (see Lambert W-function and it’s branches,

e.g. https://cs.uwaterloo.ca/research/tr/1993/03/W.pdf , chapter 4).

What we can say about $(-\sqrt{2})^{(-\sqrt{2})^{(-\sqrt{2})^\ldots}}$?

4 Answers4

Linked