3

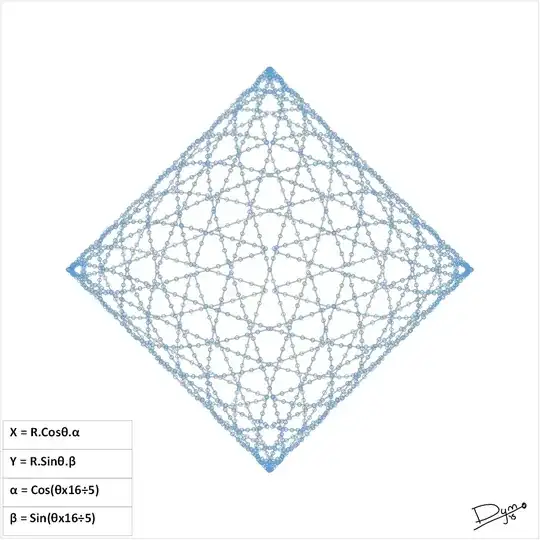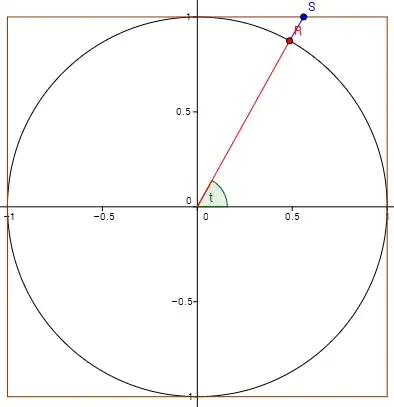
enter image description here

Given the parametric equation of a unit circle $$ \vec r(\theta) = \begin{bmatrix} \cos\theta \\ \sin\theta \end{bmatrix}, \quad 0 \leq \theta \leq 2\pi $$

It seems that there is some function $$ f : \mathbb{R} \rightarrow \mathbb{R} $$

such that $$ \vec s(\theta) = f(\theta)\vec r(\theta), \quad 0 \leq \theta \leq 2\pi $$ where $\vec s(\theta)$ is the parametric equation of a square with side length $2$.

Can this function $f$ be found, and if so, what is it?

Ryan
  • 197
  • 1
  • 5

3 Answers3

5

Such function is just:

$$ f(\theta) = \frac{1}{\max(|\sin\theta|,|\cos\theta|)}.$$

Jack D'Aurizio
  • 353,855
  • I don't doubt that this is correct, but could you provide at least an informal proof as to why? – Ryan Aug 11 '14 at 02:32
  • 3
    Such a choice can be understood in terms of the $L^\infty$ norm or supremum norm $$||\boldsymbol x||\infty = \max {|x_1|, |x_2|, \ldots, |x_n|}.$$ Then we have the natural parametrization for $n = 2$ $$\boldsymbol x (\theta) = \frac{\boldsymbol r(\theta)}{||\boldsymbol r(\theta)||\infty}$$ where $\boldsymbol r(\theta) = (\cos \theta, \sin \theta)$ is the unit circle. – heropup Aug 11 '14 at 02:35
  • 2
    Exacly, it is just the standard way to map the unit ball with respect to the euclidean norm (the circle) into the unit ball with respect to the supremum norm (the square). – Jack D'Aurizio Aug 11 '14 at 02:36
  • @Clockwise It is not difficult to prove. Try looking at just the first quadrant. The key is to observe that for $0 \le \theta < \pi/4$, $\cos \theta > \sin \theta$, and for $\pi/4 < \theta \le \pi/2$, $\sin \theta > \cos \theta$. – heropup Aug 11 '14 at 02:38
2

Found this post and thought I would share an equation I derived for "converting" a circle to a square using a ratio method that is also a parametric equation, I am sure that someone else has probably done something similar.

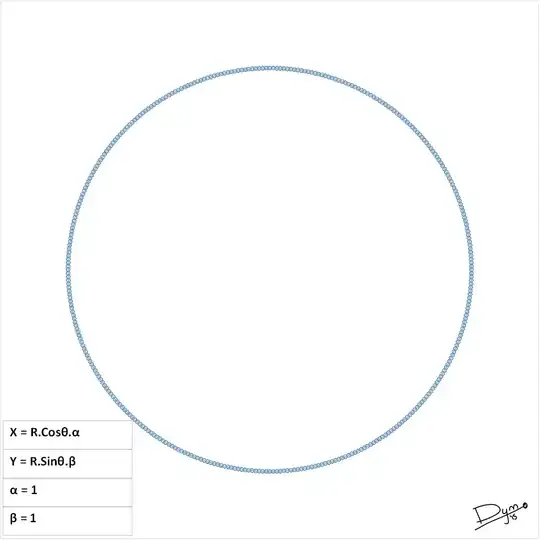
Start by plotting a circle of radius R: Parametric Equation of Circle

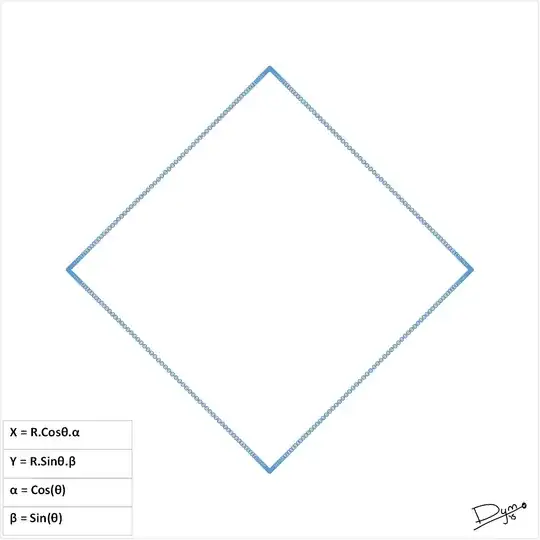
I have just given the equation, but this is represented as: Parametric Curve Representation of a Square from a Circle

You rotate the square just by offsetting theta by 45°, what also comes out of this equation is some nice plots, eg a heart: Parametric Equation of a Heart others: enter image description here

1

For the parameterization of the square, We can define such a function piecewise. For the first(and last) octant, consider that we have a right triangle, with one leg 1, the adjacent angle $\theta$. Therefore $x=1$ and $y = \tan(\theta)$.

This gives $f = \frac 1 {\cos \theta}$ on this region.

You can construct similar parameterizations for the other 4 pieces with rotations about the origin; yielding $f$ as described by Jack, $\frac{1}{\max(|\sin(\theta)|,|\cos(\theta)|)}$

Clinton Bradford
  • 964