2

I'm trying to complete Level 21 from euclid the game: http://euclidthegame.com/Level21/

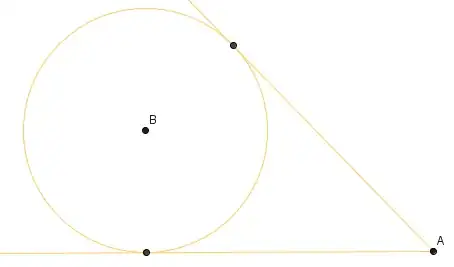
enter image description here

The goal is to construct two tangents to the given circle from the point A not on it. So far I've figured that the segments from B to the tangent points must be equal. And of course the triangles AB[tangent point] are right angles.

I'm not seeing how I can find those tangent point, a hint for a good step would be appreciated! I would rather have a hint in the sense of, this is a good step because this and that then just saying what I need to do. I could find those steps without explanation everywhere on the internet if I would like that.

Pjotr
  • 309
  • 1
  • 4
  • 8
  • On a side note, thank you so much for bringing Euclid the Game to my attention. I needed this in my life! – David H Aug 08 '14 at 19:21

3 Answers3

3

There's an interesting property that you can use for this: a triangle inscribed in a circle, with two of its points at opposite ends of a diameter of the circle, is a right triangle.

Also, a line tangent to a circle at a particular point C, makes a right angle to the radius line through C.

Try drawing a circle with diameter AB.

Dan Uznanski
  • 11,025
  • Ah cool, I got it ! How do you know that a triangle inscribed in a circle, with two of its points at opposite ends of a diameter of the circle, is a right triangle ? – Pjotr Aug 08 '14 at 19:31
  • 1
    Consider a circle with center C, diameter AB, and point on circle D. So angles DAC and ADC are the same (call it $\alpha$) because their opposite sides have the same lengths, and DBC and BDC (call it $\beta$)are the same for the same reason. Now you have ADB = $\alpha + \beta$; but ADB + DAC + DBC = $\alpha + \beta + \alpha + \beta = 2(\alpha+\beta)$ = half a circle ('cause it's a triangle), so $\alpha + \beta$ = right angle, and that's the angle at D. – Dan Uznanski Aug 08 '14 at 19:39
1

If a line from $A$ intersects a circumference in two points $P$ and $Q$ then it holds that $AP·AQ = {AT}^2$ where $T$ is a point of the circumference so that $\overline{AT}$ is tangent to the circumference.

This is called power of a point

Create such a line (for instance $\overline{AB}$). Name the points of intersection with the circumference $P$ and $Q$ where $P$ is the closest to $A$. We want $\sqrt{AP·AQ}$. You can read about the square root of the product of two segments here. I'll add the method to construct it:

Costruct the circle centered on $A$ with radius $AP$ so it intersects the line $\overline{AB}$ on $P'$.

Find the midpoint of $P'Q$, name it $M$ and construct a circle centered on $M$ with radius $MQ$.

Perpendicular to $\overline{AB}$ construct a line through $A$ that intersect the last circle on $R$ and $R'$.

Then construct a circle centered on $A$ with radius $AR$ so that intersects the circumference on $T$ and $T'$.

Construct the lines $\overline{AT}$ and $\overline{AT'}$. Those are tangent to the circumference.

Community
  • 1
Darth Geek
  • 12,296
0

The following solution reflects the figure below. What is slightly interesting about this solution is how it uses only a straightedge.

enter image description here

  1. Construct a line $x$ through the given external point $A$ and two different points $X_1$ and $X_2$ on the circle ○$B$.

  2. Construct analogous lines $y := \overleftrightarrow{AY_1Y_2}$ and $z := \overleftrightarrow{AZ_1Z_2}$.

  3. Construct lines $\overleftrightarrow {X_1Y_2}$ and $\overleftrightarrow{X_2Y_1}$. They will intersect at a point $C$.

  4. Construct lines $\overleftrightarrow {Z_1Y_2}$ and $\overleftrightarrow{Z_2Y_1}$. They will intersect at a point $D$.

  5. Construct line $\overleftrightarrow{CD}$. They will intersect ○$B$ at two points $E$ and $F$.

  6. Construct the desired lines $\overleftrightarrow{EP}$ and $\overleftrightarrow{FP}$ tangent to ○$B$ through $P$. ■

PDE
  • 1,467