5

I am able to solve equation of the type $ |5x+1|=|11-2x|$. I square both the side and my equation becomes $ (5x+1)^2=(11-2x)^2 $ further simplification gives me $ (5x+1)=\pm (11-2x)$.

I get have difficulties in solving equation of the type

$|x+1| - |1-x|=2~~$ and
$~~|x-1|=|x|+a$

Any steps and or links that could be of help will be greatly appreciated.

Arif
  • 331
  • It might help to note that $|x+1-|x-1| = \max(-2,\min(2, 2x))$. Also, $|x-1|-|x| = \max(-1, \min(1, 1-2x))$. Generally I would suggest plotting the function first. – copper.hat Aug 07 '14 at 06:23
  • Several solutions to your first problem are given here: http://math.stackexchange.com/questions/98157/how-could-we-solve-x-in-x1-1-x-2/ – Martin Sleziak Aug 07 '14 at 07:00
  • $$(5x+1)^2=(2x-11)^2$$ use different of two squares to factor this! – Bumblebee Aug 07 '14 at 03:23

4 Answers4

4

For the first one, $$|x+1| - |1-x|=2$$ Or, $$|x+1| - |x-1|=2$$ as $|x|=|-x|$, I just rearranged just because I prefer x first, not necessary; Now break a number line into three parts: Use: $|x|=\begin{cases}+x,\;x>0\\-x,\;x<0\end{cases}$

Part I:$\;x\in(-\infty,-1]$

Now, $$x+1\le0\wedge x-1<0$$

So, $$-(x+1)+(x-1)=-2$$ no solution here;

Part II:$\;x\in(-1,1]$

Now, $$x+1>0\wedge x-1\le0$$

So, $$(x+1)+(x-1)=2\implies x=1$$which is in this range;

Part III:$\;x\in(1,\infty)$

Now, $$x+1>0\wedge x-1>0$$

So, $$+(x+1)-(x-1)=2$$which is true for all x in the required range;

So, $$\large\boxed{x\in[1,\infty)}$$

Solve second one similiarly by breaking into $(\infty,0],(0,1],(1,\infty)$

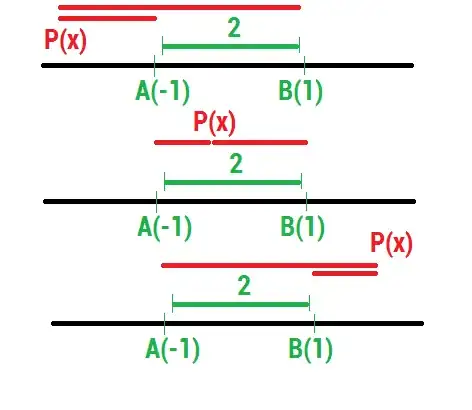
Note: There is a simpler way way for first, which is a special case: Consider it as: $$|x-(-1)|-|x-(1)|=(1)-(-1)$$ Let P(x),A(-1) and B(1) be points on number line, then: $$PA-PB=AB$$ And it is clear from the following figure that $x\in[1,\infty)$ enter image description here

RE60K
  • 17,716
2

You could use two steps of the same kind you showed before:

$|x+1|=2+|1-x|$

$x+1=2+|1-x|$ or $x+1=-2-|1-x|$

$x-1=|1-x|$ or $-x-3=|1-x|$

$x-1=1-x$ or $x-1=-1+x$ or $-x-3=1-x$ or $-x-3=-1+x$

and then solve each of these four equations seperately.

Paul Sundheim
  • 2,743
2

As explained in some answers to this question and also to How could we solve $x$, in $|x+1|-|1-x|=2$?, you can approach this geometrically.

So for the second equation $$|x-1|-|x|=a$$ you are looking for the points such that the difference between the distance from $1$ and distance from $0$ is equal to $a$.

You can also draw the graphs of the function $|x-1|$, $|x|$ and of their difference; this might help your insight into the problem.

Here are the graphs drawn by WolframAlpha.

We can see (either from graph or from geometric interpretation) that:

  • If $|a|>1$, then there are no solutions. (See also reverse triangle inequality, which implies that $|a|=||x-1|-|x||\le 1$.)
  • If $a=1$, then solutions are all numbers from the interval $(-\infty,0]$.
  • If $a=-1$, then solutions are all numbers from the interval $[1,\infty)$.
  • If $a\in(-1,1)$, then there will be exactly one solution somewhere between $0$ and $1$. I leave the details to you, but you should be able to show that $x=\frac{1-a}2$.
Community
  • 1
Martin Sleziak
  • 53,687
0

In this case, $|x + 1| - |1 - x| = 2$, we have,

$$ |x + 1| = \begin{cases} x+1 \ \text{if} \ x \geq -1\\ -x-1 \ \text{if} \ x < -1 \end{cases} \quad \text{and} \quad |1 - x| = \begin{cases} 1 - x \ \text{if} \ x \leq 1\\ x-1 \ \text{if} \ x \geq 1 \end{cases} $$ If $x < -1, \ |x + 1| =-x-1$ and $|1 - x| = 1 - x$, then $$ |x + 1| - |1 - x| = 2 \quad \Rightarrow \quad -x-1-(1 - x) = 2 \ \Rightarrow \ -2 = 2 \quad \text{Absurd!} $$ If $-1 \leq x < 1, \ |x + 1| =x + 1$ and $|1 - x| = 1 - x$, then $$ |x + 1| - |1 - x| = 2 \quad \Rightarrow \quad x + 1 - (1 - x) = 2 \ \Rightarrow \ 2x = 2 \quad \Rightarrow \quad x = 1 $$ If $x > 1, \ |x + 1| = x + 1$ and $|1 - x| = x - 1$, then $$ |x + 1| - |1 - x| = 2 \quad \Rightarrow \quad x + 1 - (x - 1) = 2 \ \Rightarrow \ 2 = 2 \quad \text{valid for all} \quad x > 1 $$ Thus, $S = \{x \in \mathbb{R} : x \geq 1\}$. The other issue resolves also analyzing cases.

Mathsource
  • 5,393