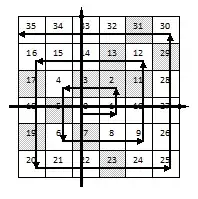
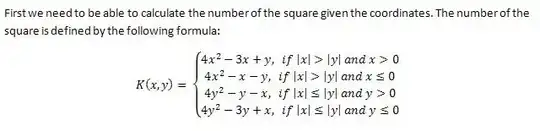3

This is the spiral

given coordinates, find the number at that coordinates in spiral matrix. Given is the image of spiral i am talking about.

at 0,0 ---> 0

0,1 ---> 1

1,1 ---> 2

0,1 ---> 3

-1,1 ---> 4

-1,0 ---> 5

-1,-1 ---> 6

And the answer is here, but i don't know how to reach to this solution. enter image description here

Somebody please give proof, how to reach to these equations.

Community
  • 1
ash
  • 41
  • In the diagram it's $(1,0) \to 1$ but your description has $(0,1) \to 1$ [and later to $3$ as in the diagram]. I once messed around with exactly this spiral, trying for the function $K(x,y)$. Interesting that someone has figured it out. – coffeemath Aug 05 '14 at 19:51

1 Answers1

1

Here's an attempted explanation of the first formula. It applies only in the open region to the right of the two lines $y=\pm x.$ If we show it is right when $y=0$ it will follow, since then the added $y$ will make it OK on the vertical line through $(x,0)$ while staying in the region.

A few sketches show that if we remove the points on the vertical line through $(x,0)$ with $y\le 0,$ what is left is a square of lattice points of side $2x-1.$ Then we need to add $x$ more, to account for the vertical part removed. But we also need to subtract one since the labeling starts at $0$ for the origin. This gives us $$(2x-1)^2+x-1=4x^2-3x,$$ which then on adding $y$ as noted to account for where one is on the last vertical part of the journey, gives the desired formula $4x^2-3x+y.$

The others are likely doable in a similar way, I'd suggest looking for a convenient point on an axis for a starting idea, and after some sketches finding a square (or maybe a rectangle near square) of lattice points which preceed your chosen axis point.

coffeemath
  • 29,884
  • 2
  • 31
  • 52