4

  1. Is there any group of order 36 with no subgroup of order 6?

  2. Is there any group of order $p^2q^2$ with no subgroup of order $pq$?

  3. Is there any group of order $p^{2m}q^{2m}$ with no subgroup of order $p^mq^m$?

  4. Is there any group of order $p^{2m}q^{2n}$ with no subgroup of order $p^mq^n$?

($p,q$ are distinct primes)

user1729
  • 31,015
M.H.Hooshmand
  • 2,537
  • 15
  • 26
  • @johnmangual: I cannot move it either, but I voted for that. I believe you can vote as well, click on "close" below the post. –  Aug 02 '14 at 20:19
  • I think we can apply Sylow's theorem and conclude that there no exist such groups for all 4 questions. – Jaehyeon Seo Aug 02 '14 at 20:36
  • In general this question is a bit deeper than one might expect (though this two prime factor case may be easier). See this recent related question for expert discussion. You see that for example with $p^mq^n=28$ or $24$ the answer is affirmative. – Jyrki Lahtonen Aug 02 '14 at 20:40
  • The answer to 1 is 'No' (see the linked question). The answer to 2 is probably also 'No', because when $p^2q^2>36$, the group has a normal $q$-Sylow subgroup ($q>p$), which should help. Hmm. May be not as that normal subgroup does not necessarily have characteristic subgroup of order $q$? – Jyrki Lahtonen Aug 02 '14 at 20:52
  • 1
    Groups of order $p^2q^2$ have been fully classified, and the answer to 2 is no for all small values of $p$ and $q$ that I tried, so I would certainly conjecture that it is no in general. I would guess that the answer to 3 is yes - I will look for an example! – Derek Holt Aug 02 '14 at 21:00

2 Answers2

5

For question 2, I believe the answer is yes, which also settles question $3$ and $4.$ Take $p = 149$ and $q = 5.$ Then a cyclic group of order $25$ acts irreducibly and faithfully on an elementary Abelian $p$-group of order $p^{2}.$ Furthermore, in the resulting semidirect product, each element of order $5$ acts irreducibly on the normal Sylow $p$-subgroup, so there is no subgroup of order $745 = pq.$

The general strategy is to find primes odd primes $p,q$ with $p \equiv -1$ mod $q^{2},$ and then a similar construction works.

Geoff Robinson
  • 24,035
4

This is not really a complete answer (yet). But since it's an interesting question and since I cannot post comments due to forum restrictions, I'll hint you to an article I found: http://matwbn.icm.edu.pl/ksiazki/fm/fm92/fm9211.pdf (if your browser doesn't display anything, try downloading).

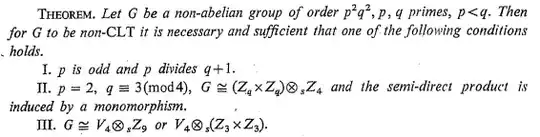
On page 2 you'll find the following theorem: Theorem from: Baskaran, S.: CLT and non-CLT groups, 1972

My knowledge of algebra is too rusty to really understand this at first glance. But a CLT-group is a group, for which the converse Lagrange Theorem holds true, so for every divisor of the group order exists a subgroup. If this paper is right, this would mean every group of order 36 is a non-CLT group (case II), so there exist at least one divisor of 36, which has no corresponding subgroup.

Since Cauchy's Theorem and Sylow Theorems imply the existence of subgroups of order 2,3,4 and 9, the divisors left are: 6,12 and 18. This doesn't directly answer your question, but the isomorphism should help finding an answer. I'll update, as soon as I find out something more precise...

kabumm
  • 121