Area of the polygon formed by cutting a cube with a plane

Question

I want to determine the area of a polygon that is formed when a cube is cut by a plane like shown below:

Where the blue triangle is in fact a part of the plane described by $$m_x x + m_y y +m_z z = \beta \tag{1} $$ and the box's dimensions are $1\times1\times1$. The polygon I am interested in is highlighted in red.

From $(1)$ I can easily determine the location of the points $r_i$ to be $$r_1=\left(0,\frac{\beta-m_z}{m_y},1\right); \;\; r_2=\left(\frac{\beta-m_z}{m_x},0,1\right); $$ $$r_3=\left(1,0,\frac{\beta-m_x}{m_z}\right); \;\; r_4=\left(1,\frac{\beta-m_x}{m_y},0\right); $$ $$r_5=\left(\frac{\beta-m_y}{m_x},1,0\right); \;\; r_6=\left(0,1,\frac{\beta-m_y}{m_z}\right); $$

I know I can determine the area of an irregular polygon with $N$ vertices located at $(a,b)$ (in some plane) as:

$$A=\frac{1}{2}\left(\sum_{i=1}^{N-1} a_i b_{i+1}-\sum_{j=1}^{N-1} a_{j+1} b_{i}+a_Nb_1-b_1a_N\right) \tag{2}$$

I somehow have to transform the coordinates $r_i$ such that they are in a plane where the third coordinate is 0, i.e. I have to align the polygon with one of the axis of my coordinate system and that is where I get stuck. How can I transform $r_i$ such that the plane aligns with my coordinate system and I can use Eq.$(2)$

P.S. I will also accept an answer with a completely different way of getting the area of the polygon, the method I describe is just the one I know of.

Answer 1

Project your polygon $P$ to the $(x,y)$-plane by forgetting the $z$-coordinates of the vertices, and compute the area of $P'$ using your formula for areas of plane polygons. Then $${\rm area}(P)={1\over\cos\phi}{\rm area}(P')\ ,$$ where $\phi$ is the angle between the $z$-axis and and the normal to the cutting plane $(1)$.

Answer 2

Method I - area from volume

Assume $m_1, m_2, m_3 > 0$ and let $\vec{m}$ be the vector $(m_1,m_2,m_3)$. WOLOG, we will assume $m_i$ are normalized such that $|\vec{m}| = 1$. Let $\theta(t)$ and $\phi(t)$ be the functions defined by

$$\theta(t) = \begin{cases}t,& t \ge 0\\0,&\text{ otherwise }\end{cases} \quad\text{ and }\quad \phi(t) = \frac{1}{6m_1m_2m_3}\theta(t)^3. $$

For any $\vec{x} = (x_1,x_2,x_3) \in \mathbb{R}^3$, consider the simplex "at" $\vec{x}$.

$$\Delta(\beta, \vec{x}) = \bigg\{\; \vec{y} = (y_1,y_2,y_3) \in \mathbb{R}^3 : y_1 \ge x_1, y_2 \ge x_2, y_3 \ge x_3\;\text{ and }\;\vec{m}\cdot\vec{y} \le \beta \;\bigg\}$$

It is easy to see

$$\text{Vol}(\Delta(\beta, \vec{x})) = \text{Vol}(\Delta(\beta - \vec{x}\cdot\vec{m}, \vec{0})) = \phi(\beta - \vec{x}\cdot\vec{m}) $$

Let use call the area we want to compute as $A(\beta)$. To compute it, we will first compute the volume of that portion of unit cube beneath the plane $\vec{x}\cdot\vec{m} \le \beta$ as a function of $\beta$. i.e.

$$V(\beta)\;\stackrel{def}{=}\;\text{Vol}( [0,1]^3 \cap \Delta(\beta,\vec{0}) )$$

Let $t$ be a variable start at $0$ and increases to its final value $\beta$.

1. For small $t$, $\Delta(t,\vec{0})$ lies completely inside the unit cube. As a result, $V(t)$ is equal to $\phi(t)$.

2. As we increases $t$, the plane $\vec{m}\cdot\vec{x} = t$ will hit one of the three vertices $(1,0,0)$, $(0,1,0)$, $(0,0,1)$ of the unit cube. Let we call this vertex $\vec{v}$. A small portion of $\Delta(t,\vec{0})$ (which itself is a simplex having $\vec{v}$ as a vertex) now lies outside the unit cube. We need to subtract its volume $\text{Vol}(\Delta(t,\vec{v})) = \phi(t -\vec{m}\cdot\vec{v}) $ from $V(t)$.

3. As we increases $t$ further, the plane $\vec{m}\cdot\vec{x} = t$ will hit one of the three vertices $(0,1,1)$, $(1,0,1)$, $(1,1,0)$. Let's say it is $\vec{w} = (1,1,0)$ that get hit. The two small simplices at $(1,0,0)$ and $(0,1,0)$ we encountered in step $2$ will now overlap. This means the subtraction of their volume from $V(t)$ in step $2$ is now an overkill. We need to add back the volume of their intersection $\text{Vol}(\Delta(t,\vec{w})) = \phi(t - \vec{m}\cdot\vec{w}))$ to $V(t)$.

As we increases $t$, the plane $\vec{m}\cdot\vec{x} = t$ will hit more and more vertices. We can organize this subtraction, add back cycle using the inclusion exclusion principle.

In the end, if we let $\vec{v}_i$, $i = 1,\ldots, 8$ be the $8$ vertices of the unit cube and $\epsilon_i$ be the corresponding parity, i.e

$$\epsilon_i = \begin{cases} 0, &\vec{v}_i = (0,0,0), (0, 1, 1), (1,0,1), (1,1,0)\\ 1, &\vec{v}_i = (1,0,0), (0, 1, 0), (0,0,1), (1,1,1) \end{cases}$$

We can express $V(\beta)$ in a compact form $$ V(\beta) = \sum_{i=1}^{8} (-1)^{\epsilon_i}\phi(\beta - \vec{m}\cdot\vec{v}_i) $$

Recall $\vec{m}$ has been normalized as an unit vector. If we increase $\beta$ for an infinitesimal amount $\delta\beta$, the change in volume will be dominated by a term proportional to $A(\beta)\delta\beta$. More precisely,

$$V(\beta + \delta\beta) - V(\beta) = A(\beta)\delta\beta + O((\delta\beta)^2)$$

This leads to a compact formula for the area we want. $$\bbox[4pt,border:1px solid blue]{ A(\beta) = \frac{dV(\beta)}{d\beta} = \frac{1}{2m_1m_2m_3}\sum_{i=1}^{8}(-1)^{\epsilon_i}\theta(\beta - \vec{m}\cdot\vec{v}_i)^2 } $$

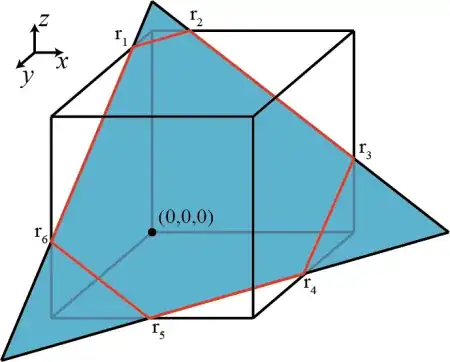
Let's use the configuration depicted in the picture in question as an example.

In that case, 4 and only 4 vertices $(0,0,0), (1,0,0), (0,1,0), (0,0,1)$ lies beneath the plane $\vec{m}\cdot\vec{x} = \beta$. RHS of above formula reduces to following quadratic polynomial in $\beta$. $$A(\beta) = \frac{1}{2m_1m_2m_3}\left[\beta^2 - (\beta-m_1)^2 - (\beta-m_2)^2 - (\beta-m_3)^2\right]$$

Method II - as a general planar polygon

Following is another way to evaluate the area. Please note that there is no need to transform points $r_i$ to a plane align to the coordinates system first.

Let $\vec{x}_1, \vec{x}_2,\ldots,\vec{x}_n$ be the vertices of a planar polygon $X$ in $\mathbb{R}^3$. Let $P$ be the plane in $\mathbb{R}^3$ holding the polygon $X$ and let $\vec{p}$ be a unit normal vector of $P$. We will assume when we view the plane $P$ from the side pointed by $\vec{p}$, the vertices $\vec{x}_1, \vec{x}_2, \ldots, \vec{x}_n$ are arranged in counter-clockwise manner. For simplicity of expression below, we will use $\vec{x}_{n+1}$ as an alias for $\vec{x}_1$.

Given any $3$ points $\vec{y}_1, \vec{y}_2, \vec{y}_3 \in P$, arranged counter-closewisely with respect to $\vec{p}$, let $A(T)$ be the area of the triangle $T$ formed by them. We have

$$\begin{align} A(T) \vec{p} &= \frac12 (\vec{y}_2 - \vec{y}_1) \times (\vec{y}_3 - \vec{y}_1)\\ \implies \quad A(T) &= \frac12\vec{p}\cdot\left[\vec{y}_1 \times \vec{y}_2 + \vec{y}_2 \times \vec{y}_3 + \vec{y}_3 \times \vec{y}_1\right] \end{align} $$

One thing you should notice is the area $A(T)$ is the sum of 3 pieces, each coming from an edge of $T$.

If we break the polygon $P$ into $n$ small triangles and apply above formula to the small triangles, the contributions form the internal edges all cancelled out. At the end, we get

$$A(P) = \frac12 \sum_{i=1}^n \vec{p} \cdot ( \vec{x}_i \times \vec{x}_{i+1})$$

This formula is very similar to what you have for polygon in $\mathbb{R}^2$. Apply these to your $r_i$, your area is equal to${}^{\color{blue}{[1]}}$

$$\frac12 \left( \begin{align} &\phantom{+} \vec{m}\cdot(r_1 \times r_2) + \vec{m}\cdot(r_2 \times r_3) + \vec{m}\cdot(r_3 \times r_4) \\ &+ \vec{m}\cdot(r_4 \times r_5) + \vec{m}\cdot(r_5 \times r_6) + \vec{m}\cdot(r_6 \times r_1)\end{align} \right) $$ If you substitute your expression of $r_i$ into it and throw the mess to a CAS, it can be simplified to something like $$\begin{align}&\frac{m_1^2+m_2^2+m_3^2}{2m_1m_2m_3} \left( -2b^2 + 2(m_1+m_2+m_3)b - (m_1^2+m_2^2+m_3^2)\right)\\ = &\frac{1}{2m_1m_2m_3}\left(b^2 - (b-m_1)^2 - (b-m_2)^2 - (b-m_3)^2\right) \end{align} $$ Reproducing what we get by method I.

Notes

• $\color{blue}{[1]}$ Please note that in the your picture, $r_1, r_2, \ldots, r_6$ are ordered clockwisely with respect to $\vec{m}$. If that is really the case, one should add an minus side to the area. However, you have drawn your coordinate system opposite to the usual convention. If you draw your picture in the usual right-handed coordinate system, they will be ordered counter-clockwisely instead of clockwisely.

Answer 3

This argument is specifically for the case in which the plane's intersection with the cube is a hexagon.

---

Let the plane meet the coordinate axes as $A = (a,0,0)$, $B = (0,b,0)$, $C = (0,0,c)$, so that its equation can be written $$\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1$$ (In terms of your notation, this means $a = \beta/m_x$, $b = \beta/m_y$, $c = \beta/m_z$.) Capitalizing your $r_i$ for notational consistency, the area you seek is $$|\triangle ABC| - |\triangle AR_3R_4| - |\triangle BR_5R_6| - |\triangle CR_1R_2| \qquad(\star)$$

Note that each of the triangles referenced in $(\star)$ is the "hypotenuse-face" of a right-corner tetrahedron. Moreover, the tetrahedra are similar, so that the areas in question are related by (the squares of) appropriate proportions of the corresponding dimensions measured along coordinate axes. For instance, with $O = (0,0,0)$ and $I = (1,0,0)$, we have $$|\triangle AR_3R_4| = \left(\frac{|AI|}{|AO|} \right)^2 |\triangle ABC| = \frac{\;(a-1)^2}{a^2}|\triangle ABC|$$ and likewise for $|\triangle BR_5R_6|$ and $|\triangle CR_1R_2|$, so that $(\star)$ becomes $$|\triangle ABC|\left( 1 - \frac{(a-1)^2}{a^2} - \frac{(b-1)^2}{b^2} - \frac{(c-1)^2}{c^2}\right) \qquad (\star\star)$$

Now, to get $|\triangle ABC|$ itself, we simply apply the Pythagorean-like Theorem of de Gua for right-corner tetrahedra, which gives the square of the hypotenuse-area as the sum of the squares of the (easily-computed) leg-areas: $$|\triangle ABC|^2 = |\triangle OBC|^2 + |\triangle OCA|^2 + |\triangle OAB|^2 = \frac{1}{4}\left( b^2c^2 + c^2 a^2 + a^2 b^2 \right)$$

The makes $(\star\star)$ equal to $$\frac{1}{2}\sqrt{ b^2c^2 + c^2 a^2 + a^2 b^2}\;\left( 1 - \frac{(a-1)^2}{a^2} - \frac{(b-1)^2}{b^2} - \frac{(c-1)^2}{c^2}\right)$$ $$= \frac{\beta^2 \sqrt{m_x^2 + m_y^2 + m_z^2}}{2m_x m_y m_z} \frac{1}{\beta^2}\left(-2 \beta^2 + 2 \beta (m_x+m_y+m_z) - ( m_x^2 + m_y^2 + m_z^2)\right)$$ $$= \frac{\sqrt{m_x^2 + m_y^2 + m_z^2}}{2m_x m_y m_z}\left(-2 \beta^2 + 2 \beta (m_x+m_y+m_z) - ( m_x^2 + m_y^2 + m_z^2)\right) \qquad (\star\star\star)$$

This agrees with @achillehui's answer, under the assumption that $m_x^2 + m_y^2 + m_z^2 = 1$.