I have around 1000 values for a gps receiver position like follows: All of these values represent the SAME POINT.
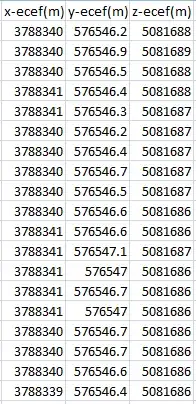
want to find error in values? What I am doing right now is that I am finding cartesian distance between the actual value and the mean value of all 1000 readings. Then I am representing cartesian distance on a graph so it represents error. I dont think this is the right approach. What formulaes should I use or methods I should employ to show error with the readings.