Solving equations with dozens of ceil and floor functions efficiently?

Question

I am tackling a problem which uses lots of equations in the form of:

$$ q_i(x) = c_i(x) + \sum_{j=1}^N \left\lfloor \frac{q_i(x)}{P_j} \right\rfloor C_j $$

where $q_i(x)$ is the only unknown, $c_i$, $C_j$, $P_j$ are always positive. $C_j < P_j$ for all $j$

1. How is this type of problems efficently solved especially when the number of iterations $N$ is between 20 - 100?

What I was doing is $q_i(x) - c_i(x)$ must be equal to the summation of integers. So i was doing an exhaustive search for $q_i(x)$ which satisfies both ends of the equation. Clearly this is computationally exhaustive even if I do the search on a parallel computer..

1. What if $c_i(x)$ is a floating point number, this will even make the problem even more difficult to find a real $q_i(x)$?

Thanks

Answer 1

It is confusing to write $q_i(x)$ and $c_i(x)$ when they are really just numbers. I suppose this problem is part of a larger problem where you're trying to solve many such equations. Anyhow, let me rewrite your equation as $$Q = C + \sum_{j = 1}^N \left\lfloor \frac{Q}{P_j} \right\rfloor C_j$$ where

• $Q$ is the unknown number (you wrote $q_i(x)$)
• $C$ is a positive number (you wrote $c(x)$)
• $P_j$'s and $C_j$'s are positive numbers and $C_j < P_j$ for all $j$.

Define the function $f$ to be $$f(x) = C + \sum_{j = 1}^N \left\lfloor \frac{x}{P_j} \right\rfloor C_j.$$ We are trying to solve $$Q = f(Q)$$ which is a fixed point equation. The function $f$ is monotonically increasing. To get some feel for it, let's consider the example $C = 11$, $N = 10$, $P_j = 10 j + 1$ and $C_j = 2 j$. We draw the graph of $y = f(x)$ and $y = x$, and observe where they intersect (magenta is $f$):

As you see, there are several solutions. There is a well-known method for finding fixed points of functions:

1. Start with an arbitrary approximation, say $X_0 = 0$
2. Define $X_{k+1} = f(X_k)$
3. Keep computing $X_0$, $X_1$, $X_2$, ... until you get $X_{k+1} = X_k$, or at least $|X_{k+1} - X_k| < \epsilon$ for an acceptably small $\epsilon$.

There is no guarantee the process will actually find a fixed point, but at least in our case it does, we get: $X_0 = 0$, $X_1 = 11$, $X_2 = 13$, $X_3 = 13$, so $X = 13$ is a solution. Depending on what your $P_j$ and $C_j$ look like this method may work well.

Answer 2

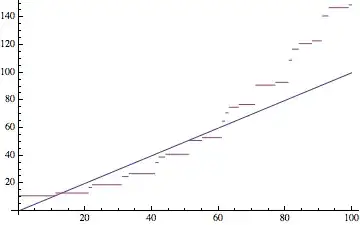
My proposal:

[For the sake of brevity the unknown $q_i(x)$ is denoted $Q$ and $c_i(x)$, $C$.] All constants can be real.

The right hand side is a sum of regular staircase functions, with the steps having width $P_j$ and height $C_j$. You can construct the resulting sum for increasing $Q$, from $Q=0$, by finding all discontinuities. The discontinuities occur at integer multiples of the widths, i.e. $k_jP_j$.

Maintain a vector with components $(k_j+1)P_j$, and a corresponding sum $S=C+\sum k_jC_j$. Initialize all $k_j=0$ and $S=C$. Now take the smallest of the $(k_j+1)P_j$ and increment $k_j$: $k_jP_j$ is increased by $P_j$, and $S$ by $C_j$.

Doing this repeatedly, you will enumerate all discontinuities, by increasing order. Between two successive discontinuities, let at $Q'$ and $Q''$, the sum is constant and equals the current S. You have a solution $Q=S$ every time that $Q'\le S\le Q''$.

For efficient implementation, the list of future discontinuities $(k_j+1)P_j$ is better organized as a priority queue.

Assuming that the first solution is found after the $M^{th}$ discontinuity, the running time will be $O(M\log N)$.

UPDATE:

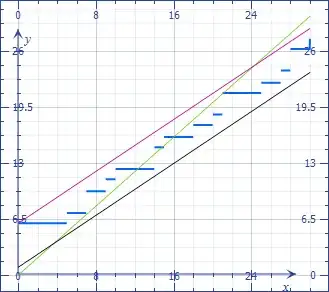
Given that $x-1<\lfloor x\rfloor\le x$, we have this bracketing for $S$: $$C+Q\sum_{j=1}^N\frac{C_j}{P_j}-\sum_{j=1}^NC_j<S=C+\sum_{j=1}^N\lfloor\frac Q{P_j}\rfloor C_j\le C+Q\sum_{j=1}^N\frac{C_j}{P_j}.$$

By equating the bounds (magenta and black lines) to $Q$ (green), you get a good estimate of the range where solutions can be found. (If you start from a nonzero $Q$, you can initialize $k_j=\lfloor\frac Q{P_j}\rfloor$.)

Answer 3

Not sure if this helps for your set of parameters, but it is an alternative view on the problem.

This system can be written as: $$ \begin{align} q_i(x) &= c_i(x) + \sum_{j=1}^N \left\lfloor \frac{q_i(x)}{P_j} \right\rfloor C_j \\ &= c_i(x) + \sum_{j=1}^N \left( \frac{q_i(x)}{P_j} -f_j \right) C_j \\ &= c_i(x) + q_i(x) \sum_{j=1}^N \frac{C_j}{P_j} - \sum_{j=1}^N \frac{C_j}{P_j} f_j \end{align} $$ with $$ f_j:f_j(q_i(x)) = \mbox{frac}\left(\frac{q_i(x)}{P_j}\right) \in [0, 1) $$

And this gives another fixed point equation $$ q_i(x) = \frac{c_i(x)-r f(q_i(x))}{1 - s(r)} =: \Phi(q_i(x)) \quad (*) $$ (with $r_j = C_j / P_j >0$ and $s(r) = \sum_{i=1}^N r_j> 0$) if $s(r) \ne 1$. For $s(r) < 1$ we get $$ q_i(x) \in \left( \frac{c_i(x)}{1-s(r)}-\frac{s(r)}{1-s(r)}, \frac{c_i(x)}{1-s(r)} \right] $$ and for $s(r) > 1$ we get $$ q_i(x) \in \left[ -\frac{c_i(x)}{s(r)-1}, -\frac{c_i(x)}{s(r)-1} + \frac{s(r)}{s(r)-1}\right) $$

For $s(r) = 1$ one has to solve $$ r f(q_i(x)) = c_i(x) $$