Equation of rectangle

Question

I need equation of a rectangle on the Cartesian coordinate system. Is there an equation for a rectangle? for example equation of ellipse is $$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$

Answer 1

There is no simple equation By that I mean that there is no "nice" function $f(x,y)$ for which $f(x,y)=0$ would determine a rectangle. Of course such a function exists, it's just not useful or nice to look at. For example, for the square with edges $(-1,-1),(-1,1),(1,-1),(1,1)$, you can take the function $$f(x,y) = \max\{|x|,|y|\} - 1$$ which yields the square when equaled to $0$.

You can now stretch and move this function, so $f(x-a, y-b) = 0$ will create a square with sides of length $2$ and center at $(a,b)$. $f(\frac xc,\frac yd) = 0 $ will create a square with sides $c,d$ centered at the origin. $f(\frac{x-a}c, \frac{y-b}d$ will create a rectangle with sides $c,d$, centered at $a,b$.

That said, I think a much better way of describing such rectanles is $[a,b]\times [c,d]$ (for the full rectangle, or the edge of this set for the edge alone).

Answer 2

For a rectangle centered at $(a,b)$ with $l=$ side length parallel to the $x$-axis and $m=$ side length parallel to the $y$-axis, the equation is $$\text{Max} \biggl( \frac{2 \, |x-a|}{l}, \frac{2 \, |x-b|}{m} \biggr)= 1 $$

Answer 3

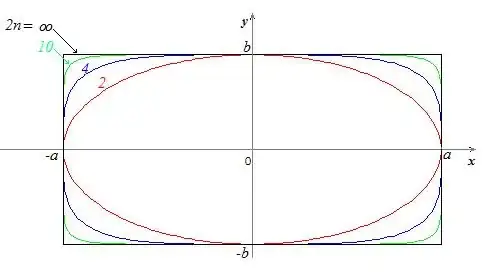
A curious equation : $$\lim_{n \to \infty}\left({\left(\frac{x}{a}\right)^{2n} + \left(\frac{y}{b}\right)^{2n}}\right) = 1$$ For $-a<x<a$ then $\frac{x^2}{a^2}<1$ then $\left(\frac{x^2}{a^2}\right)^\infty=0$. Hense $\frac{y^2}{b^2}=1$ . So $y=b$ or $y=-b$ which gives the upper and the lower sides of the rectangle.

For $-b<y<b$ then $\frac{y^2}{b^2}<1$ then $\left(\frac{y^2}{b^2}\right)^\infty=0$. Hense $\frac{x^2}{a^2}=1$ . So $x=a$ or $x=-a$ which gives the right and the left sides of the rectangle.

http://mathworld.wolfram.com/Superellipse.html

http://mathworld.wolfram.com/Rectellipse.html

Answer 4

The answers above kind of look more complex than needed so here is my take on the problem. We begin with absolute value function to form a diamond shape: $$y(x)=|x|\Rightarrow |x|+|y|=a\sqrt{2}\Rightarrow\text{Cylindrical coordinates}$$ The reason behind this step is for us to rotate it by 45 degrees: $$|r\text{cos}\phi|+|r\text{sin}\phi|=a\sqrt{2}\Rightarrow\phi\rightarrow\phi+\frac{\pi}{4}$$ $$\Rightarrow|r\text{cos}(\phi)-r\text{sin}(\phi)|+|r\text{cos}(\phi)+r\text{sin}(\phi)|=2a$$ Since we rotated it 45 deg. we must now revert it to Cartesian coordinates: $$|x-y|+|x+y|=2a$$ Now we have a square with side $a$ but we got to stretch it in the $x$ direction. To do this we simply substitute $x\rightarrow \frac{a}{b}x$ as if we shrank it earlier to get a square. And voila! We get the equation for a rectangle with centre in (0,0) and with sides a,b in Cartesian coordinates: $$|ax-by|+|ax+by|=2ab$$

You can check desmos to make a plot of this equation!