How to put 9 pigs into 4 pens so that there are an even number of pigs in each pen?

Question

Put 9 pigs into 4 pens so that there are an even number of pigs in each pen.

Read this for inspiration.

Answer 1

Put 9 pigs into 4 pens so that there are an even number of pigs in each pen.

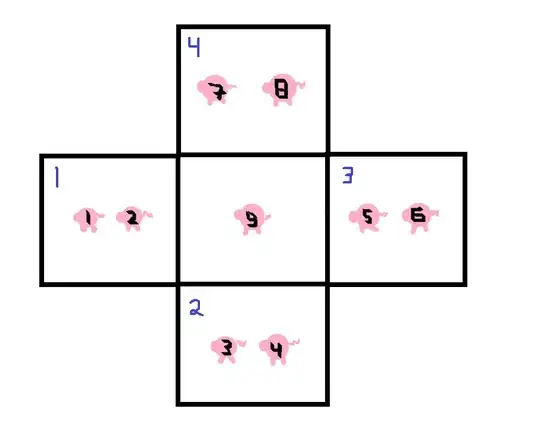
Using an analogous example to the odd number of pigs per pen, we can see each pen has an even number of pigs. The last pig is liberally interpreted as being 'put into' the four pens. Though it isn't inside one of the four pens, it is inside the four pens.

Answer 2

Lemma: $-\frac{1}{12}$ is an integer.

Proof: Consider the Riemann zeta function $\zeta$ evaluated at $-1$. By analytic continuation, $\zeta(-1) = -\frac{1}{12}$. However, we also have the series expansion $\zeta(s)=\displaystyle \sum_{n=1}^\infty n^{-s}$, so (ignoring issues with convergence), $\zeta(-1)=1+2+3+\cdots$. This is an infinite sum of integers. Any finite sum of integers is an integer, and the since the integers are a closed set (and hence contain all limit points) this also holds in the limiting case. Hence $-\frac{1}{12}$ is an integer.

Corollary: $1$ is even.

Proof: By above, since $-\frac{1}{12}$ is an integer, $12 (-\frac{1}{12})=-1$ is an even integer. Since the successor of the successor of any even integer is even, $-1+1+1=1$ is even.

Theorem: It is possible to put 9 pigs in 4 pens such that each pen has an even number of pigs.

Proof: For the first pen, put $8$ of the pigs in. For the second pen, put $1$ (which is even by our corollary) pig in it. For the remaining two pens, put no pig in them.

Note: The above is adapted humor of Logan Maingi.

Answer 3

If you overlap two pens, like a Venn diagram, you can put one pig in each of the three compartments (hence two pigs in each pen, with one pig counted twice). Then put two more pigs in a (disjoint) third pen and the final four in a fourth.