Is there a differentiable function $f$ in which the differential function $f'$ is bounded but has no maximum on one closed interval? Thanks
-
2Impossible, differentiable implies continuous. – Adam Hughes Jul 27 '14 at 22:53
-
@masoud: Are u looking for some differentiable function $f$ which $f'$ is bounded and has no max on any closed intervals? – Mikasa Jul 27 '14 at 23:15
-
I think something like $f(x) = -x|x|+x^2\sin(1/x)$ would also work. – Jonas Meyer Jul 28 '14 at 03:43
2 Answers
Answer assuming looking for "at least one closed interval":
Define the sequence $a_{n}=\frac{1}{3^{n}}$. Then $s_{k}=\sum\limits_{i=k}^{\infty}a_{i}=\frac{3}{2\times 3^{k}}$. Hence $\lim\limits_{k\rightarrow\infty}\frac{s_{k}}{(\frac{1}{2^{k+1}})}=\lim\limits_{k\rightarrow\infty}3(\frac{2}{k})^{k}=0$.
Define a collection of function $g_{k}:[\frac{1}{2^{k}},\frac{1}{2^{k+1}}]\rightarrow\mathbb{R}$ to be a nonnegative continuous function that vanish at 2 endpoints and have the maximum value being $1-(\frac{1}{4})^{k}$ and also $\int\limits_{\frac{1}{2^{k}}}^{\frac{1}{2^{k+1}}}g(t)dt=a_{k}$. (it is easy to show that those $g_{k}$ exist, as we give it plenty of room to get the integral it needed, and obtaining a maximum value is just a matter of putting a small spike).
Define $g:[-1,1]\rightarrow\mathbb{R}$ to be $g(0)=0$ and $g(x)=g_{k}(|x|)$ if $|x|\in[\frac{1}{2^{k}},\frac{1}{2^{k+1}}]$.
Define $f:[-1,1]\rightarrow\mathbb{R}$ to be $f(x)=\int\limits_{0}^{x}g(t)dt$.
Now calculate $f^{\prime}(0)=\lim\limits_{h\rightarrow 0}\frac{\int\limits_{0}^{h}g(t)dt}{h}$. We have for $h\in[\frac{1}{2^{k}},\frac{1}{2^{k+1}}]$ then $0\leq\frac{\int\limits_{0}^{h}g(t)dt}{h}<\frac{s_{k}}{(\frac{1}{2^{k+1}})}$. Since $\lim\limits_{k\rightarrow\infty}\frac{s_{k}}{(\frac{1}{2^{k+1}})}=0$ by squeeze theorem we have $f^{\prime}(0)=\lim\limits_{h\rightarrow 0}\frac{\int\limits_{0}^{h}g(t)dt}{h}=0$.
As for $f^{\prime}(x)$ when $x\not=0$, notice that $g$ is continuous on $[-1,0)$ and $(0,1]$ so $f^{\prime}(x)=g(x)$.
Hence $f^{\prime}=g$.
Now notice that $g$ do not have any maximum on $[-1,1]$, since its values approach $1$ arbitrarily close, but it never take that values.
Hence $f$ is what we are looking for.
- 5,338
-
-
@masoud: sorry I got an error, that doesn't work on all closed interval. I added a proof on why no $f$ exist if we require that condition on all closed interval. – Gina Jul 28 '14 at 01:34
-
1This function $f$ is only differentiable a.e. I believe the OP wanted a function that's differentiable everywhere. – Jul 28 '14 at 01:38
-
-
@ Gina: I need only for one interval not for all nondegenerated intervals and also I need a function differentiable everywhere, not only almost every where. – Fin8ish Jul 28 '14 at 01:48
-
@masoud: I changed my example and undelete my answer. This should work now. – Gina Jul 28 '14 at 02:48
-
"...discontinuous only on a meagre set, there exist nondegenerated closed interval that contains no points of discontinuity." This is not true. In general, a meagre set can be dense, and in particular, there are derivatives that are discontinuous on a dense set. E.g., there are everywhere differentiable but nowhere monotone functions. – Jonas Meyer Jul 28 '14 at 03:03
-
@JonasMeyer: you means Weierstrass function's derivative is discontinuous on a dense set? I never knew that...Oh well, this answer will soon break my record for number of edits to fix maths errors :( – Gina Jul 28 '14 at 03:09
-
@Gina: I don't know what you mean. The "Weierstrass function" that comes to mind is continuous but nowhere differentiable, so isn't relevant here. But there are less well known differentiable functions whose derivatives are discontinuous on a dense set. I don't know if any are called Weierstrass functions. – Jonas Meyer Jul 28 '14 at 03:18
-
@JonasMeyer: oh sorry I got confused. Then what would be an example of those functions? – Gina Jul 28 '14 at 03:21
-
@Gina: Here is a reference: http://mathoverflow.net/questions/167323/everywhere-differentiable-function-that-is-nowhere-monotonic. Here is another: http://math.stackexchange.com/questions/17067/differentiablenot-monotone. Because a function whose derivative is continuous in a nondegenerate interval must be monotone in some subinterval, a differentiable function that is nowhere monotone has a derivative with discontinuities in all intervals (in case the relevance of the links was in question). – Jonas Meyer Jul 28 '14 at 03:24
-
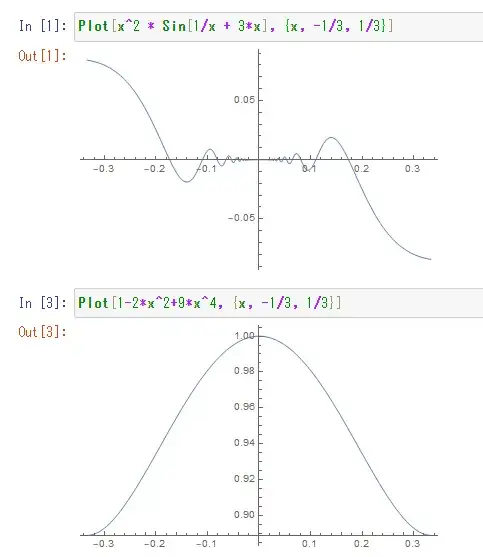
I found this example in "An introduction to Analysis"(in Japanese) by Ichiro Tajima.
$$f(x)=\begin{cases} x^2 \sin (\frac{1}{x} + 3 x), \ x\in [-\frac{1}{3}, 0) \cup (0, \frac{1}{3}]\\ 0, \ x = 0\end{cases}.$$
$$f'(x)=\begin{cases} 2 x \sin (\frac{1}{x} + 3 x) + (3 x^2 - 1) \cos (\frac{1}{x} + 3 x), \ x\in [-\frac{1}{3}, 0) \cup (0, \frac{1}{3}]\\ 0, \ x = 0\end{cases}.$$
If $x \neq 0$, then $$f'(x) = \sqrt {1 - 2 x^2 + 9 x^4} \sin (\frac{1}{x} + 3 x + \alpha(x)).$$
And $g(x) := 1 - 2 x^2 + 9 x^4$ attains the maximum value at $x = 0$.
So, $$\{f'(x) \mid x \in [-\frac{1}{3}, \frac{1}{3}]\} = (-1, 1).$$
- 8,690