inverse trigonometric equation $\tan^{-1}{x}+\cot^{-1}{x}=\frac{\pi}{2}$

Question

I have problem with showing that $\displaystyle \tan^{-1}{x}+\cot^{-1}{x}=\frac{\pi}{2}$ I think there have to be used formula: $\displaystyle \tan(\alpha+\beta)=\frac{\tan{\alpha}+\tan{\beta}}{1-\tan{\alpha}\tan{\beta}} $ but I don't know how to apply it and yet I don't know whether it's true that $\displaystyle\cot^{-1}{x}=\frac{1}{\tan^{-1}{x}}$ ?

The last is not right. But, since $\cot y = \frac{1}{\tan y}$, you have $\cot^{-1} x = \tan^{-1} \frac{1}{x}$. — Daniel Fischer, Jul 25 '14 at 12:58
Taking the tangent of both members will lead you nowhere, as $\tan\frac\pi2$ is not defined. — , Jul 25 '14 at 13:05

score 3 · Accepted Answer · edited Apr 13 '17 at 12:21

Let $y = \arctan x$, then \begin{align} \tan y&=x\\ \frac{1}{\tan y}&=\frac{1}{x}\\ \cot y&=\frac{1}{x}\\ \tan\left(\frac\pi2-y\right)&=\frac{1}{x}\\ \frac\pi2-y&=\arctan\left(\frac{1}{x}\right)\\ \frac\pi2-\arctan x&=\text{arccot}\ x\\ \large\color{blue}{\arctan x+\text{arccot}\ x}&\color{blue}{=\frac\pi2}.\qquad\qquad\blacksquare \end{align} Here is the link for the proof of $\ \arctan\left(\frac1x\right) = \text{arccot}(x)$.

score 1 · Answer 2 · answered Jul 25 '14 at 13:22

1

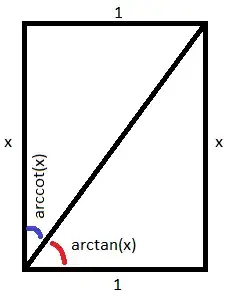
Note $\pi/2$ is $90^\circ$. Consider the rectangle in the following diagram: enter image description here

answered Jul 25 '14 at 13:22

bonsoon

3,059

2

Don't understand the downvotes here! This is a very nice geometric way of seeing why the identity is true. – Winther Jul 25 '14 at 13:40

score 0 · Answer 3 · answered Jul 25 '14 at 13:04

0

The correct identity should be $$\cot^{-1}{x}=\tan^{-1}\left(\frac{1}{x}\right)$$ The equation becomes $$\tan^{-1}{x}+\tan^{-1}\left(\frac{1}{x}\right)=\frac{\pi}{2}$$ We will take the tangent then the inverse tangent of the LHS to get \begin{align} \tan^{-1}\left(\tan\left(\tan^{-1}{x}+\tan^{-1}\left(\frac{1}{x}\right)\right)\right) &=\tan^{-1}\left(\frac{x+1/x}{1-1}\right) \end{align} Clearly the term inside is not defined, and this occurs at $\dfrac{(2n+1)\pi}{2}$. But since the domain of the function $\tan^{-1}{x}$ is restriced to $-\dfrac{\pi}{2}\le 0 \le \dfrac{\pi}{2}$, we can say $$\tan^{-1}{x}+\tan^{-1}\left(\frac{1}{x}\right)=\frac{\pi}{2}$$

answered Jul 25 '14 at 13:04

SuperAbound

5,554

How did you obtain the term $\displaystyle\frac{(2n+1)\pi}{2}$ ?? – Gregor Jul 25 '14 at 13:18
You can obtain it simply by observing the where the asymptotes are on the graph of $y=\tan{x}$. Alternatively, these are just the roots of $\cos{x}$ – SuperAbound Jul 25 '14 at 13:18
But $\tan^{-1}(1/x) = \cot^{-1}(x)$ so the stated identity is correct! – Winther Jul 25 '14 at 13:38
The stated identity is indeed correct. That is what I have just shown. Since the LHS is equal to an inverse tangent of a undefined value, this means that it can only be $\dfrac{\pi}{2}$ due to the restricted domain of the inverse tangent function. – SuperAbound Jul 25 '14 at 13:49

score 0 · Answer 4 · answered Jul 25 '14 at 13:39

A calculus proof:

Let $f(x)=\arctan(x)+\textrm{arcot}(x)$ for all $x\in {\mathbb R}$. The function $f$ is differentiable and $f'(x)=\frac{1}{1+x^2}+\frac{-1}{1+x^2}=0$, so $f$ is constant. The value of the constant is $f(0)=\arctan(0)+\textrm{arccot}(0)=0+\frac{\pi}{2}$ (remember that $\tan(0)=0$ and $\cot(\frac{\pi}{2})=0$), so $\arctan(x)+\textrm{arccot}(x)=\frac{\pi}{2}$ for all $x\in {\mathbb R}$.

Note: I prefer the notation $\arctan$ over $\tan^{-1}$ since it helps to avoid mistakes like $\cot^{-1}(x)=\frac{1}{\tan^{-1}(x)}$.

Edit: the precalculus tag was added while I was writing my answer.

inverse trigonometric equation $\tan^{-1}{x}+\cot^{-1}{x}=\frac{\pi}{2}$

4 Answers4