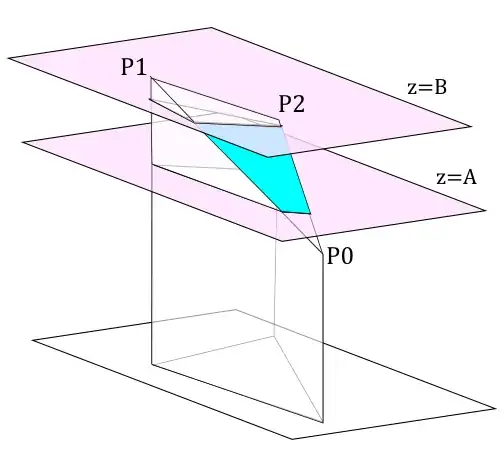
The fraction of the triangle's area between the two planes is given by:
$$
\frac{(B-z_0)^2 - (A-z_0)^2}{(z_1-z_0)(z_2-z_0)}
$$
In your example, $z_0 = 900$, $z_1 = 1500$, $z_2 = 1200$, $A = 1100$ and $B= 1200$. So the fraction of area is:
$$
\begin{align}
\frac{(1200 -900)^2 + (1100-900)^2}{(1500 - 900)(1200-900)} &= \frac{300^2-200^2}{600\times300}\\
& = \frac{90\ 000 - 40\ 000}{600\times 300} \\
&= \frac{50\ 000}{180\ 000}\\
&=\frac{5}{18}\\
&= 27.7\%
\end{align}
$$
PROOF:
Fistly note that if $Q_{1}$ is a point on the line $P_0P_1$ then it has the form $Q_1=P_0 + t_1(P_1 - P_0)$ for some $t_1$ and if $Q_2$ is a point on the line $P_0P_2$ then it has the form $Q_2P_0 + t_2(P_2 - P_0)$ for some $t_2$.
Consider the triangle $Q_1P_0Q_2$. The area of this triangle can be found from the length of the cross product of the two vectors $P_0Q_1$ and $P_0Q_2$.
Now $P_0Q_1 = Q_1- P_0 = P_0 + t_1(P_1 - P_0) - P_0 = t_1(P_1-P_0)$, so we have
$$
P_0Q_1 = t_1(P_1-P_0)\\
P_0Q_2 = t_2(P_2-P_0)\\
$$
and so
$$
\begin{align}
P_0Q_1 \times P_0Q_2 &= t_1(P_1-P_0) \times t_2(P_2-P_0)\\
&= t_1 t_2 (P_1 \times P_2 - P_1 \times P_0 - P_0 \times P_2 - P_0 \times P_0)\\
&= t_1 t_2 (P_1 \times P_2 - P_0 \times P_2 + P_2 \times P_0)
\end{align}
$$
Thus the area of the triangle $Q_1P_0Q_1$ is given by:
$$
\text{Area of } Q_1P_0Q_1 = \frac{1}{2}t_1t_2 | P_1 \times P_2 - P_0 \times P_2 + P_2 \times P_0 |
$$
For convenience, we will denote by $W$ the quantity $\frac{1}{2}| P_1 \times P_2 - P_0 \times P_2 + P_2 \times P_0 |$.
Denote by $P_{1A}$ the point where $P_0P_1$ meets the plane with equation $z=A$,
by $P_{2A}$ the point where $P_0P_2$ meets the plane with equation $z=A$,
by $P_{1B}$ the point where $P_0P_1$ meets the plane with equation $z=B$,
and by $P_{2B}$ the point where $P_0P_2$ meets the plane with equation $z=B$.
$P_{1A}$ has coordinates $P_0 + t_{1A}(P_1 - P_0)$ for some $t_{1A}$. The third coordinate must be $A$ so that $z_0 + t_{1A}(z_1 - z_0) = A$. Thus $t_{1A}=\frac{A - z_0}{z_1 - z_0}$. Similarly we have the following:
$$
P_{1A} = P_0 + t_{1A}(P_1 - P_0) \quad \text{where } t_{1A} = \frac{A-z_0}{z_1-z_0}\\
P_{2A}= P_0 + t_{2A}(P_2 - P_0) \quad \text{where } t_{2A} = \frac{A-z_0}{z_2-z_0}\\
P_{1B} = P_0 + t_{1B}(P_1 - P_0) \quad \text{where } t_{1B} = \frac{B-z_0}{z_1-z_0}\\
P_{2B} = P_0 + t_{2B}(P_2 - P_0) \quad \text{where } t_{2B} = \frac{B-z_0}{z_2-z_0}\\
$$
Also observe that: $P_1 = P_0 + 1(P_1 - P_0)$ and $P_2 = P_0 + 1(P_2-P_0)$.
Hence by the argument above we have:
$$
\text{Area of } P_1P_0P_2 = 1\cdot 1 W = W\\
\text{Area of } P_{1B}P_0P_{2B} = t_{1B}t_{2B}W\\
\text{Area of } P_{1A}P_0P_{2A} = t_{1A}t_{2A}W
$$
The blue-shaded area in the diagram is therefore given by:
$$
\begin{align}
\text{Area between the two planes} &= t_{1B}t_{2B} W - t_{1A}t_{2B} W \\
&= (t_{1B}t_{2B} - t_{1A}t_{2B}) W\\
&= \left( \frac{B-z_0}{z_1-z_0} \frac{B-z_0}{z_2 - z_0} - \frac{A-z_0}{z_1 - z_0} \frac{A - z_0}{z_2 - z_0}\right) W\\
&= \left( \frac{(B- z_0)^2}{(z_1 - z_0)(z_2-z_0)} - \frac{(A-z_0)^2}{(z_1-z_0)(z_2-z_0)}\right) W\\
&= \frac{(B-z_0)^2 - (A - z_0)^2}{(z_1-z_0)(z_2-z_0)}W
\end{align}
$$
The area of the whole triangle $P_1P_0P_2$ is $W$ and so the fraction of area that is between the two planes is therefore given by:
$$
\text{Fraction of triangle's area between the two planes} = \frac{(B-z_0)^2 - (A-z_0)^2}{(z_1-z_0)(z_2-z_0)}
$$