7

Problem :

Number of non zero integer values of $k$ for which the points ($k,k^2)$ lies inside the triangle formed by the lines $11x+6y+14=0$, $9x+y-12=0$, $2x+5y-17=0$

(a) $0$

(b) $2$

(c) $3$

(d) $4$

I have no clue on this how to solve this problem, request you to please suggest thanks.

najayaz
  • 5,459
user108258
  • 1,372
  • How about drawing the three lines on squared paper ? Then count the points $(k,l)$ within, where $k,l$ are positive integers; and then the ones with $l=k^2$. – Dietrich Burde Jul 21 '14 at 15:25
  • Use the idea from http://math.stackexchange.com/questions/190111/how-to-check-if-a-point-is-inside-a-rectangle – lab bhattacharjee Jul 21 '14 at 15:31

2 Answers2

5

If you study a little about straight lines and co-ordinate geometry, you will see that points on the same side of a straight line always have same sign of the function for that line. What I mean to say is, for a line $ax+by+c=0$, suppose a point ($x_1,y_1$) lies on the right of this line. Now if you put ($x_1,y_1$) in the expression, suppose $ax_1+by_1+c$ comes out to be positive. Now if another point ($x_2,y_2$) gives a positive value of $ax_2+by_2+c$, then it will also lie on the right side of the line.

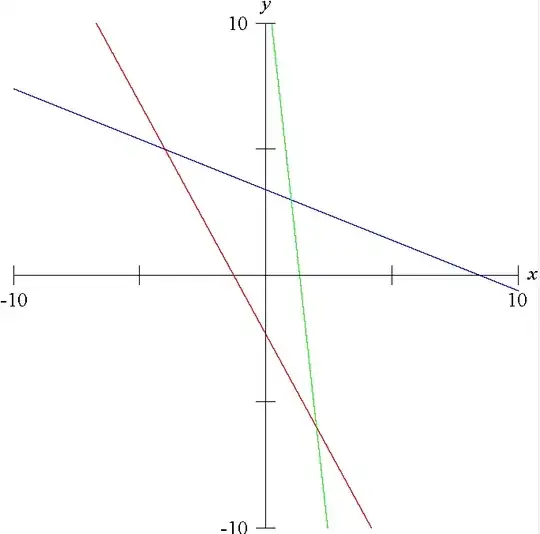
Now, if you graph those lines, you can see that the origin lies inside the triangle: enter image description here

So using the above theory, the point ($k,k^2$) should have the same sign as the constants in the equations of the lines. Then we have: $$11k+6k^2+14>0$$ $$9k+k^2-12<0$$ $$2k+5k^2-17<0$$ If you solve those inequalities, you will get a range for k and then it is an easy task to get the integer values. I think the you will get only 2 values of k.

najayaz
  • 5,459
1

First of all you have to calculate all the vertices by intersecting each line with the other ones.

Once you have the vertices, you have the bounding box of the triangle: max and min in x and max and min in y. With that you can discard any $(k, k^2)$ where $k > x_{max}$ or $k < x_{min}$ or $k^2 > y_{max}$ or $k^2 < y_{min}$.

With the remaining pairs $(k, k^2)$ you can calculate the barycentric coordinates for each one to know if they are inside the triangle.

Jordi Cruzado
  • 321