Calculate control points of cubic bezier curve approximating a part of a circle

Question

I'm not mathematically inclined, so please be patient with my question.

Given

• $(x_0, y_0)$ and $(x_1, y_1)$ as the endpoints of a cubic Bezier curve.

• $(c_x, c_y)$ and r as the centerpoint and the radius of a circle.

• $(x_0, y_0)$ and $(x_1, y_1)$ are on the circle.

• if it makes the calculation simpler, it's safe to assume the arc is less than or equal to $\frac{\pi}{2}$.

How do I calculate the two control points of the Bezier curve that best fits the arc of the circle from $(x_0, y_0)$ to $(x_1, y_1)$?

Answer 1

Let $(x,y)^R=(-y,x)$ represent rotation by $\pi/2$ counterclockwise and $$ \gamma(t)=(1-t)^3p_0+3t(1-t)^2p_1+3t^2(1-t)p_2+t^3p_3 $$ define a cubic bezier with control points $\{p_0,p_1,p_2,p_3\}$.

Suppose $p_0=(x_0,y_0)$, $p_3=(x_1,y_1)$, and $c=(c_x,c_y)$ are given so that $|p_0-c|=|p_3-c|=r$ ($p_3$ is counterclockwise from $p_0$). Then $p_1=p_0+\alpha(p_0-c)^R$ and $p_2=p_3-\alpha(p_3-c)^R$ where $$ \alpha=\frac43\tan\left(\frac14\cos^{-1}\left(\frac{(p_0-c)\cdot(p_3-c)}{r^2}\right)\right) $$ For a quarter of a circle, $\alpha=\frac43(\sqrt2-1)$, and $\gamma$ is no more than $0.00027$ of the radius of the circle off.

Here is a plot of $\gamma$ in red over the quarter circle in black. We really don't see the circle since it is no more than $0.1$ pixels off from $\gamma$ when the radius is $400$ pixels.

$\hspace{3.5cm}$

---

Computation of $\boldsymbol{\alpha}$

Looking at an arc with an angle of $\theta=\cos^{-1}\left(\frac{(p_0-c)\cdot(p_3-c)}{r^2}\right)$

$\hspace{1.5cm}$

we see that the distance from $c$ to the middle of the arc is $$ r\cos(\theta/2)+\frac34\alpha r\sin(\theta/2) $$ we wish to choose $\alpha$ so that this is equal to $r$. Solving for $\alpha$ gives $$ \begin{align} \alpha &=\frac43\frac{1-\cos(\theta/2)}{\sin(\theta/2)}\\ &=\frac43\tan(\theta/4) \end{align} $$

---

A Slight Improvement

Using a circle of radius $1$, the maximum error in radius produced using $\alpha=\frac43\tan(\theta/4)$ is approximately $$ 0.0741\cos^4(\theta/4)\tan^6(\theta/4) $$ and the error is always positive; that is, the cubic spline never passes inside the circle. Reducing $\alpha$ reduces the midpoint distance by $\frac34\sin(\theta/2)=\frac32\tan(\theta/4)\cos^2(\theta/4)$ times as much, so to distribute the error evenly between the positive and negative, a first guess, assuming that the amplitude of the radius is unchanged, would be to reduce $\alpha$ by $0.0247\cos^2(\theta/4)\tan^5(\theta/4)$.

A bit of investigation shows that, when equalizing the positive and negative swings of the radius, the amplitude increases and that $$ \alpha=\frac43\tan(\theta/4)-0.03552442\cos^2(\theta/4)\tan^5(\theta/4) $$ gives pretty even distribution of the error between positive and negative for $\theta\le\pi/2$. The maximum error, both positive and negative, is approximately $$ 0.0533\cos^4(\theta/4)\tan^6(\theta/4) $$ When $\theta=\pi/2$, this agrees with the article mentioned by bubba in comments.

Note however, that in minimizing the radial error from the circle, the actual variation in radius is increased. Using the simple formula for $\alpha$, which puts the cubic bezier outside the circle, the radius varies by $0.0741\cos^4(\theta/4)\tan^6(\theta/4)$. However, when we minimize the error, the radial variation increases to $0.1066\cos^4(\theta/4)\tan^6(\theta/4)$.

Answer 2

As a different way to choose where the error falls, one could pick the control points such that the enclosed area matches that of the circle.

If we consider the first quarter of a circle (the same as the first image in the other answer), then the area should be $\pi/4$, so we need the integral

$$ \begin{align} \pi/4 &= \int_{0}^{1} y(t)x'(t)dt \\ &= \int_{0}^{1} ( (1-t)^3 + 3(1-t)^2t + 3(1-t)t^2c )( 3(1-t)^2c + 6(1-t)t(1-c) ) dt \\ &= -\frac{3c^2}{20}+\frac{3c}{5} + \frac12 \\ c &= 2 - \sqrt{\frac13(22-5\pi)} \\ &≈ 0.5517784778... \end{align} $$

That's slightly smaller than the other two answers, as it attempts to even out the error between over- and under-shooting the circle, rather than minimizing the maximum error.

Aside: Edits appreciated to add a solution for angles other than 90°. My maths are rusty.

Answer 3

I got inspired to attempt yet another way to interpret "best fit": most-constrained curvature.

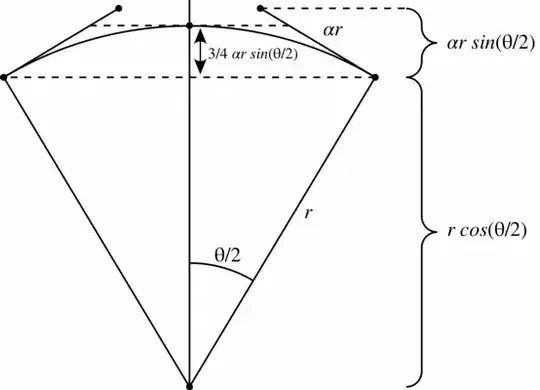
Let's look at the first quarter-circle, using the four control points $<1,0>$, $<1,α>$, $<α,1>$, $<1,0>$.

$$ \begin{align} x(t) &= (1-t)^3 + 3 (1-t)^2 t + 3 α (1-t) t^2 \\ y(t) &= 3 α (1-t)^2 t + 3 (1-t) t^2 + t^3 \\ &= x(1-t) \\ k(t) &= \frac{ x' y'' - y' x'' }{ (x'^2 + y'^2)^{3/2} } \\ &= \frac{ -18(2α(t - 1)t + αt^2 - 2(t - 1)t)(2α(t - 1) + αt - 2t + 1) + 18(α(t - 1)^2 + 2α(t - 1)t - 2(t - 1)t)(α(t - 1) + 2αt - 2t + 1) } { 27((α(t - 1)^2 + 2α(t - 1)t - 2(t - 1)t)^2 + (2α(t - 1)t + αt^2 - 2(t - 1)t)^2)^{3/2} } \end{align} $$

Where $k(t)$ is the signed curvature, but since we're going clockwise it'll be positive.

As is usually the case, the curvature expression is horrible, so we need a more tractable way forward.

Thinking about the extreme cases, a lower value of $α$ (like $0.1$) will make the ends turn sharply to get a flat middle while a high value of $α$ (like $1$) will make flat ends thus causing a pointy middle.

Graphing the curvature for a few values of $t$ helps confirm that intuition (source)

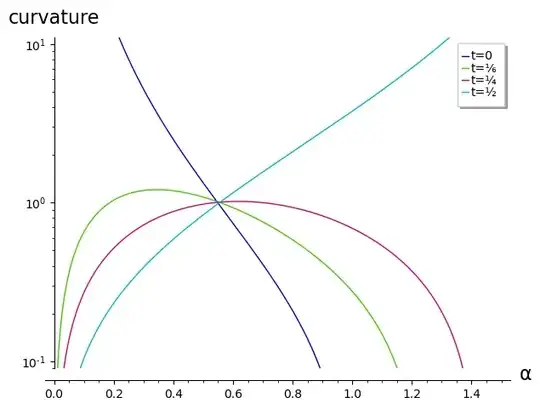
($t > 1/2$ not included on the chart due to symmetry.)

Since we're approximating a unit circle we're hoping to get $k(t) ≈ 1$, and those lines seem to intersect around there, at roughly $t ≈ 0.55$.

To balance out the extremes, we can pick $α$ such that ends and the middle have the same curvature. To avoid weird curves we'll require $α \in (0, 1)$, which simplifies a few things

$$ \begin{align} k(0) = k(1) &= k(1/2) \\ \frac{-2(α-1)}{3α^2} &= \frac{ 8\sqrt{2} α }{ 3(α-2)^2 } \\ {-2 (α-1) }{ 3(α-2)^2 } &= { 8\sqrt{2} α }{3α^2} \\ α &≈ 0.550581172753306 \end{align} $$

That value gives curvature within about $±1\%$ for $t \in [0, 1]$ (source)

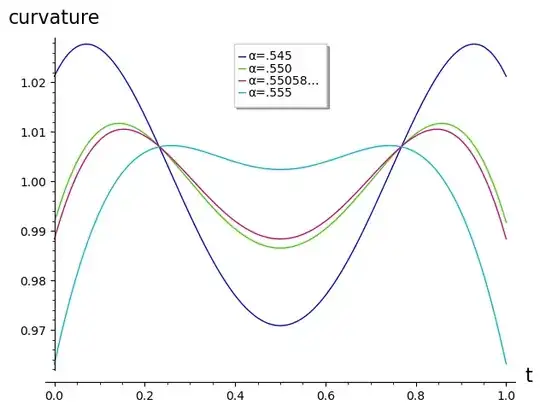
Exercise for the reader: Convince a CAS to compute

$$ \int_0^1 (k(t) - 1)^2 \mathrm{d}t $$

or

$$ \int_0^1 log(k(t))^2 \mathrm{d}t $$

and find the value of $α$ that actually minimizes the error in curvature -- it probably gives a slightly different value from the one I computed here.