I disagree with @MarkFantini's answer.
In this section ($\S$1.II.2 Moving Particle Argument), Needham is giving a heuristic argument in support of the fact that $e^{i \theta} = \cos \theta + i \sin \theta$. He has not defined $e^{i \theta}$ to be $\cos \theta + i \sin \theta$, and in fact he argues that doing so is "a low blow to Euler, reducing one of his greatest achievements to a mere tautology" ($\S$1.II.1 Introduction, page 10).
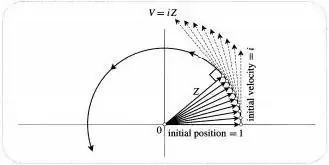
Instead, what Needham is arguing in $\S$1.II.2 is that if we suppose that it makes sense to talk about $e^{it}$, then a natural property we would want it to have is $\frac{d}{dt}e^{it} = i e^{it}$ (eq. (11) on page 11), analogous to the known property of the real exponential function, namely $\frac{d}{dx} e^{kx} = k e^{kx}$ for any real $k$.
Now, visualizing the function $t \mapsto e^{it}$ as describing the motion of a moving particle in the plane, the quantity $\frac{d}{dt} e^{it}$ is then the velocity of the particle. We know that multiplication by $i$ corresponds to a rotation of the plane by $\pi/2$ radians in the counter-clockwise direction. So, the position and velocity vectors are at right angles to each other at every point. From this, and the fact that at $t = 0$ the particle is at $e^0 = 1$, one can deduce that the particle is just moving around the unit circle.
Hence, $\lvert e^{it} \rvert = 1$ for all $t$.