I think about solution to this system of congruence. Could you give me a clue ?
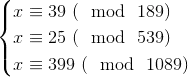
I think about solution to this system of congruence. Could you give me a clue ?
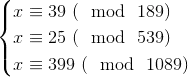
Each of the modulus bases shares prime factors with each of the other bases, which yields more congruncy than would be the case for three coprime bases.
1089 --> 3, 3, 11, 11
189 --> 3, 3, 3, 7
589 --> 7, 7, 11
Consider the first few positive numbers which equal 399 mod 1089:
399
1488
2577
3666
4755
What is the 539 modulus of these numbers?
399 --> 399
1488 --> 410
2577 --> 421
3666 --> 432
4755 --> 443
Do you see a pattern?
Every number is 3 mod 11. 25 and 399 are also 3 mod 11. Therefore, the continuation of this sequence will necessarily produce 25 mod 539 periodically - every 49th number, in fact.
When will this pattern reach a congruence?
(25 - 399) mod 539 = 165
165/11 = 15
This is how many times you must add 1089 to 399 to get 25 mod 539
399 + 15 * 1089 = 16734
16734 is the lowest number which is both 399 mod 1089 and 25 mod 539.
When will it happen again? And how often will it produce a number which is 39 mod 189?
Find the least common multiple of 1089 and 539. Adding this number will produce each next lowest congruence for these two conditions.
...
The LCM of 1089 and 539 is found by dividing one of the numbers by their common prime, 11, and then multiplying what remains: 53361
By the way, what prime factors of 189 does this number share?
...
Add 53361 to 16734:
16734
70095
123456
176817
230178
283539
How many of these are going to be 39 mod 189?
...
Every third number above is also 39 mod 189. Congruences for all three conditions will show up on an interval determined by the LCM of 1089, 539, and 189, which is 160083.